题目内容
16.观察下列两组算式.解答下列问题:第一组:$\sqrt{{2}^{2}}$=2,$\sqrt{(-2)^{2}}$=2,$\sqrt{{5}^{2}}$=5,$\sqrt{(-5)^{2}}$=5,$\sqrt{{0}^{2}}$=0
第二组:($\sqrt{2}$)2=2,($\sqrt{3}$)2=3,($\sqrt{9}$)2=9,($\sqrt{16}$)2=16,($\sqrt{0}$)2=0
(1)由第一组可得结论.对于任意实数a,有$\sqrt{a^2}$=|a|
(2)由第二组可得结论:当a≥0时.($\sqrt{a}$)2=a
(3)利用(1)、(2)的结论计算:
$\sqrt{(-0.289)^{2}}$=0.289,($\sqrt{0.289}$)2=0.289
(4)化简:当x<2时,计算$\sqrt{(x-2)^{2}}$的值.
分析 (1)通过观察即可解决.
(2)通过观察即可解决.
(3)直接利用公式计算即可.
(4)根据公式$\sqrt{{a}^{2}}$=|a|即可即可.
解答 解:(1)由第一组可得结论.对于任意实数a,有$\sqrt{{a}^{2}}$=|a|.
故答案为$\sqrt{{a}^{2}}$=|a|.
(2)由第二组可得结论:当a≥0时,($\sqrt{a}$)2=a,
故答案为($\sqrt{a}$)2=a.
(3)$\sqrt{(-0.289)^{2}}$=0.298,($\sqrt{0.289}$)2=0.298.
故答案为0.298,0.298.
(4)∵x<2,
∴原式=$\sqrt{(x-2)^{2}}$=|x-2|=2-x.
点评 本题考查二次根式的乘除法,记住公式($\sqrt{a}$)2=a(a≥0):$\sqrt{{a}^{2}}$=|a|,注意两个公式不能混淆,属于基础题,中考常考题型.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5.下列三条线段不能组成直角三角形的是( )
| A. | a=8,b=15,c=17 | B. | a=9,b=12,c=15 | C. | a=9,b=40,c=41 | D. | a:b:c=2:3:4 |
6.若a=-0.22,b=-2-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则它们的大小关系是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
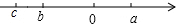 a,b,c在数轴上的位置如图,化简|a+b|+|b+c|-|a-c|-|a+c|.
a,b,c在数轴上的位置如图,化简|a+b|+|b+c|-|a-c|-|a+c|. 如数轴所示,化简:|-m-m|=-2m.
如数轴所示,化简:|-m-m|=-2m.