题目内容
14.在等边△ABC中,作以DB为直角边的等腰Rt△DBC(A、D两点在BC的同侧),则∠ADB=135°.分析 根据等边三角形的性质得出∠A=∠B=∠C=60°,AB=AC,根据等腰直角三角形的性质得出BD=DC,∠DBC=∠DCB=45°,进一步证得△ABD≌△ACD,得出∠BAD=∠CAD=$\frac{1}{2}$∠A=30°,然后根据三角形内角和定理即可求得.
解答 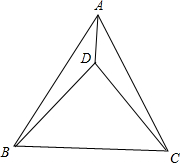 解:如图,∵△ABC是等边三角形,
解:如图,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=AC,
∵在等边△ABC中,作以DB为直角边的等腰Rt△DBC(A、D两点在BC的同侧),
∴∠BDC=90°,BD=DC,
∴∠DBC=∠DCB=45°,
∴∠ABD=∠ACD=15°,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴∠BAD=$\frac{1}{2}$∠A=30°,
∴∠ADB=180°-30°-15°=135°.
故答案为135°.
点评 本题考查了等边三角形的性质,等腰直角三角形的性质,三角形内角和定理以及三角形全等的判定和性质,熟练掌握性质和定理是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.下列二次根式中,与$\sqrt{8}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
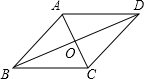 如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
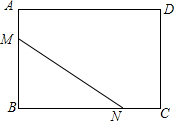 如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$. 将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°.
将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°.