题目内容

15．化简$\frac{a-b}{\sqrt{a}+\sqrt{b}}$，甲、乙两同学的解法如下：
甲：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$=$\frac{（a-b）（\sqrt{a}-\sqrt{b}）}{（\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）}$=$\frac{（a-b）（\sqrt{a}-\sqrt{b}）}{a-b}$=$\sqrt{a}$$-\sqrt{b}$；
乙：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$=$\frac{（\sqrt{a}）^{2}-（\sqrt{b}）^{2}}{\sqrt{a}+\sqrt{b}}$=$\frac{（\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）}{\sqrt{a}+\sqrt{b}}$=$\sqrt{a}$-$\sqrt{b}$．
对于甲、乙两同学的解法，正确的判断是（　　）
A．甲、乙的解法都不正确B．甲正确、乙不正确
C．甲不正确、乙正确D．甲、乙都不正确

分析 利用分子，分母同时乘以有理化因式或分子化为含有分母的乘积形式求解．

解答 解：甲：当a=b时，原式分子、分母都乘以$\sqrt{a}-\sqrt{b}$后分母为0，无意义；
乙：将分子利用平方差公式分解，正确；
故选：C．

点评 本题主要考查了分母有理化，解题的关键是正确找出有理化因式或把分子化为含有分母的乘积形式．

练习册系列答案
相关题目
5．如图，抛物线C1：y=x2+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C1向右平移m（m＞0）个单位得到抛物线C2，C2交x轴于A、B两点（点A在点B的左边），交y轴于点c．
（1）求抛物线C1的解析式及顶点坐标．
（2）以AC为直角边向上作直角三角形ACD（∠CAD是直角），且tan∠DCA=$\frac{1}{2}$，当点D落在抛物线C2的对称轴上时，求抛物线C3的解析式．
（3）若抛物线C2的对称轴上存在点P，并且以P为圆心AC长为半径的圆经过A，C两点，求m的值．
6．下列二次根式中，与$\sqrt{8}$是同类二次根式的是（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{5}$D．$\sqrt{6}$
3．将一矩形纸条按如图所示折叠，若∠1=40°，则∠2=110°．
10．已知：抛物线y=x2+（m+1）x+$\frac{1}{2}$m+$\frac{1}{4}$（m≠0）．
（1）求此抛物线与x轴的交点个数；
（2）抛物线恒过定点A，求A点坐标；
（3）求证：随着m的变化，产生的一系列抛物线的顶点都在一条确定的函数图象上，求此函数解析式．
20．如图，在△ABC中，BE是它的角平分线，∠C=90°，D在AB边上，以DB为直径的半圆O经过点E．求证：AC是⊙O的切线．
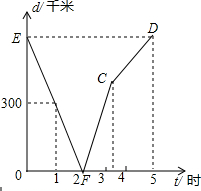7．甲、乙两列火车分别从A，B两城同时相向匀速驶出，甲车开往终点B城，乙车开往终点A城，乙车比甲车早到达终点；如图所示，是两车相距的路程d（千米）与行驶时间t（小时）的函数的图象．
（1）经过2小时两车相遇；
（2）A，B两城相距600千米路程；
（3）分别求出甲、乙两车的速度；
（4）分别求出甲车距A城的路程s甲、乙车距A城的路程s乙与t的函数关系式；（不必写出t的范围）
（5）当两车相距200千米路程时，求t的值．
16．观察下列两组算式．解答下列问题：
第一组：$\sqrt{{2}^{2}}$=2，$\sqrt{（-2）^{2}}$=2，$\sqrt{{5}^{2}}$=5，$\sqrt{（-5）^{2}}$=5，$\sqrt{{0}^{2}}$=0
第二组：（$\sqrt{2}$）2=2，（$\sqrt{3}$）2=3，（$\sqrt{9}$）2=9，（$\sqrt{16}$）2=16，（$\sqrt{0}$）2=0
（1）由第一组可得结论．对于任意实数a，有$\sqrt{a^2}$=|a|
（2）由第二组可得结论：当a≥0时．（$\sqrt{a}$）2=a
 （3）利用（1）、（2）的结论计算：
$\sqrt{（-0.289）^{2}}$=0.289，（$\sqrt{0.289}$）2=0.289
（4）化简：当x＜2时，计算$\sqrt{（x-2）^{2}}$的值．
17．在下列四个数中，比0小的数是（　　）
A．0.2B．|-1|C．$\root{3}{-8}$D．$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网