题目内容
15.第一个图形为矩形,依次连矩形各边的中点得到第二个图形(菱形),按照此方法继续下去.已知第一个图形的面积为3,则第n个图形的面积为($\frac{3}{2}$)2n-2.
分析 易得第二个矩形的面积为($\frac{1}{2}$×3)2,第三个矩形的面积为($\frac{1}{2}$×3)4,依此类推,第n个矩形的面积为($\frac{1}{2}$×3)2n-2.
解答 解:已知第一个矩形的面积为3.
第二个矩形的面积为原来的($\frac{1}{2}$×3)2×2-2=$\frac{1}{4}$×32;
第三个矩形的面积是($\frac{1}{2}$×3)2×3-2=$\frac{1}{16}$×32;
…
故第n个矩形的面积为:($\frac{1}{2}$×3)2n-2.
故答案为:($\frac{3}{2}$)2n-2.
点评 本题考查了三角形的中位线定理及矩形、菱形的性质,是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.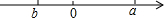 若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
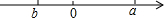 若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )
若实数a、b在数轴上的位置如图所示,则代数式|b-a|+$\sqrt{{a}^{2}}$化简为( )| A. | b | B. | b-2a | C. | 2a-b | D. | b+2a |

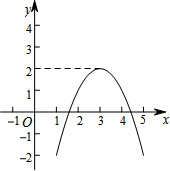 对某一个函数给出如下定义:如果存在实数M,对于任意的函数值y,都满足y≤M,那么称这个函数是有上界函数,在所有满足条件的M中,其最小值称为这个函数的上确界.例如,图中的函数是有上界函数,其上确界是2.
对某一个函数给出如下定义:如果存在实数M,对于任意的函数值y,都满足y≤M,那么称这个函数是有上界函数,在所有满足条件的M中,其最小值称为这个函数的上确界.例如,图中的函数是有上界函数,其上确界是2. 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件:
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件: 如图,直线l上依次有三个点O,A,B,OA=40cm,OB=160cm.
如图,直线l上依次有三个点O,A,B,OA=40cm,OB=160cm.