题目内容
20．设a、b是两个任意独立的一位正整数，则点（a，b）在抛物线y=ax2-bx的上方的概率是$\frac{19}{81}$．分析 首先根据题意列出表格，然后由表格即可求得所有等可能的结果与点（a，b）在抛物线y=ax2-bx的上方的情况，再利用概率公式即可求得答案．
解答 解：列表得：
| 9 | （1，9） | （2，9） | （3，9） | （4，9） | （5，9） | （6，9） | （7，9） | （8，9） | （9，9） |
| 8 | （1，8） | （2，8） | （3，8） | （4，8） | （5，8） | （6，8） | （7，8） | （8，8） | （9，8） |
| 7 | （1，7） | （2，7） | （3，7） | （4，7） | （5，7） | （6，7） | （7，7） | （8，7） | （9，7） |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） | （7，6） | （8，6） | （9，6） |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） | （7，5） | （8，5） | （9，5） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） | （7，4） | （8，4） | （9，4） |
| 3 | （1，30 | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） | （7，3） | （8，3） | （9，3） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） | （7，2） | （8，2） | （9，2） |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） | （7，1） | （8，1） | （9，1） |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
∴点（a，b）在抛物线y=ax2-bx的上方的概率是：$\frac{19}{81}$．
故答案为：$\frac{19}{81}$．
点评 此题考查了列表法或树状图法求概率与二次函数的性质．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
如图，在梯形ABCD中，AD∥BC，AD=3，AB=CD=4，∠A=120°，则下底BC的长为
．
8．|-9|的平方根等于（ ）
| A． | ±3 | B． | 3 | C． | ±$\sqrt{3}$ | D． | $\sqrt{3}$ |
12．某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶，然后以每瓶6元的价格出售，如果当天卖不完，剩余的只有倒掉．店主记录了30天的日需求量（单位：瓶），整理得下表：
（1）求这30天内日需求量的众数；
（2）假设鲜奶店在这30天内每天购进28瓶，求这30天的日利润（单位：元）的平均数；
（3）以30记录的各需求量的频率作为各需求是发生的概率．若鲜奶店每天购进28瓶，求在这记录的30天内日利润不低于81元的概率．
| 日需求量 | 26 | 27 | 28 | 29 | 30 |
| 频数 | 5 | 8 | 7 | 6 | 4 |
（2）假设鲜奶店在这30天内每天购进28瓶，求这30天的日利润（单位：元）的平均数；
（3）以30记录的各需求量的频率作为各需求是发生的概率．若鲜奶店每天购进28瓶，求在这记录的30天内日利润不低于81元的概率．
9．2014年天津市全市经济运行情况显示，天津市2014年实现地区生产总值（GDP）15722.47亿元，其中15722.47用科学记数法表示为（ ）
| A． | 1.572247×105 | B． | 15.72247×103 | C． | 1.572247×104 | D． | 15.72247×102 |
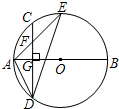如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}=\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=$\frac{\sqrt{5}}{4}$；④S△DEF=4$\sqrt{5}$，其中正确结论的个数是（ ）