题目内容
 已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E.
已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E.(1)求证:△ABD∽△CBE;
(2)求线段BE的长度.
考点:相似三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)由AB=AC,AD平分∠BAC,证出AD⊥BC,得出∠ADB=∠CEB,再由∠B=∠B,证出△ABD∽△CBE;(2)由△ABD∽△CBE,根据对应边成比例求出BE的长.
解答:(1)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=
BC=6,
∴∠ADB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠ADB=∠CEB,
又∵∠B=∠B,
∴△ABD∽△CBE;
(2)解:∵△ABD∽△CBE,
∴
=
,
即
=
,
∴BE=
.
∴AD⊥BC,BD=CD=
| 1 |
| 2 |
∴∠ADB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠ADB=∠CEB,
又∵∠B=∠B,
∴△ABD∽△CBE;
(2)解:∵△ABD∽△CBE,
∴
| AB |
| BC |
| BD |
| BE |
即
| 8 |
| 6 |
| 3 |
| BE |
∴BE=
| 9 |
| 4 |
点评:(1)本题考查了等腰三角形的性质、相似三角形的判定与性质的综合运用;关键是掌握三角形相似的判定方法,根据相似三角形求出线段的长.

练习册系列答案
相关题目
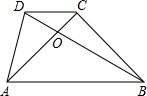 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |
 如图,拦水坝的横断面为梯形ABCD,根据图中的数据求:
如图,拦水坝的横断面为梯形ABCD,根据图中的数据求: 根据图,回答下列问题:
根据图,回答下列问题: 如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线
如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线 如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.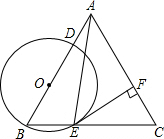 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.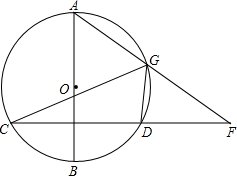 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是