题目内容

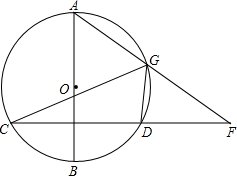如图，已知AB是⊙O的直径，弦CD⊥AB于点E，G是
AD
上一点，AG、CD的延长线相交于点F，求证：∠FGD=∠AGC．
考点：圆周角定理,垂径定理,圆内接四边形的性质
专题：证明题
分析：连接AC，根据四边形ACDG是圆内接四边形可知∠FGD=∠ACD．再由垂径定理得出
AC
=
AD
，故∠AGC=∠ACD，利用等量代换即可得出结论．
解答：证明：连接AC，
∵四边形ACDG是圆内接四边形，
∴∠FGD=∠ACD．
∵弦CD⊥AB于点E，
∴
AC
=
AD
，
∴∠AGC=∠ACD，
∴∠FGD=∠AGC．
点评：本题考查的是圆周角定理，根据题意作出辅助线，构造出圆内接四边形是解答此题的关键．
练习册系列答案
相关题目
已知：如图，在△ABC中，AB=AC=8cm，BC=6cm，AD平分∠BAC，CE⊥AB交AB于E．
（1）求证：△ABD∽△CBE；
（2）求线段BE的长度．
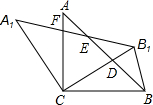如图，在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点C逆时针旋转α角（0°＜α＜90°），得到△A1B1C，连接BB1，设CB1交AB于D，A1B1分别交AB，AC于E，F
（1）求证：△CBD≌△CA1F；
（2）试用含α的代数式表示∠B1BD；
（3）当α等于多少度时，△BB1D是等腰三角形．
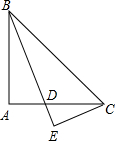已知：△ABC是等腰直角三角形，∠A=90°，BD平分∠ABC交AC于点D，CE⊥BD．
求证：BD=2CE．
在一个不透明的袋子中，有2个白球和2个红球，它们只有颜色上的区别，从袋子中随机地摸出一个球记下颜色放回．再随机地摸出一个球．则两次都摸到白球的概率为
 
．
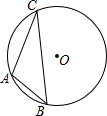如图，⊙O为△ABC的外接圆，
AC
=2
AB
，tan∠ABC=
2
2
，求tan∠C的值．
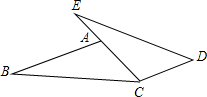如图，E、A、C三点共线，AB∥CD，∠B=∠E，AC=CD，求证：BC=ED．
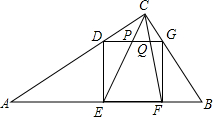如图，△ABC中，∠C=90°，AC=4，BC=3，正方形DEFG的四个顶点分别在边AC、AB、CB上．
（1）求证：△ADE∽△GBF；
（2）求正方形DEFG的边长；
（3）连结CE、CF分别交DG于点P、Q．求证：PQ2=PD•QG．
如图是一个正方体的表面展开图，如果正方体相对的面上标注的值相等，那么x+2y=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网