题目内容
 如图,拦水坝的横断面为梯形ABCD,根据图中的数据求:
如图,拦水坝的横断面为梯形ABCD,根据图中的数据求:(1)坡角∠B和∠C;(精确到0.1°)
(2)坝顶宽AD和斜坡AB的长;(精确到0.1m)
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)根据坡度的定义再利用计算器得出坡角α和β的度数;
(2)利用勾股定理得出AB的长,进而得出EC的长即可得出BC的长;
(2)利用勾股定理得出AB的长,进而得出EC的长即可得出BC的长;
解答:解:(1)∵i=1:1.5,
∴tanα=
=
,
故α≈21.1°,
∵i=1:3,
∴tanα=
,
故β≈15°;

(2)∵AF=6m,i=1;1.5,
∴BF=9m,
故AB=
=3
≈3.6(m),
∵AF=DE=6m,i=1;3,
∴EC=18m,
∴AD=FE=BC-BF-EC=30-18-9=3(m),
∴坝顶宽3米,斜坡坡AB长为3.6米.
∴tanα=
| 1 |
| 1.5 |
| 2 |
| 3 |
故α≈21.1°,
∵i=1:3,
∴tanα=
| 1 |
| 3 |
故β≈15°;

(2)∵AF=6m,i=1;1.5,
∴BF=9m,
故AB=
| 62+92 |
| 13 |
∵AF=DE=6m,i=1;3,
∴EC=18m,
∴AD=FE=BC-BF-EC=30-18-9=3(m),
∴坝顶宽3米,斜坡坡AB长为3.6米.
点评:此题主要考查了坡度的定义以及勾股定理的应用,根据已知坡度定义得出BF,EC的长是解题关键.

练习册系列答案
相关题目
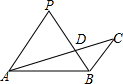 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的( )


| A、①② | B、③② | C、①④ | D、③④ |
 如图,直线y=
如图,直线y=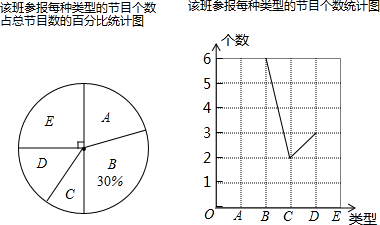
 已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E.
已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E.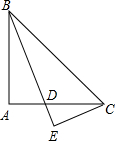 已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.
已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.