题目内容
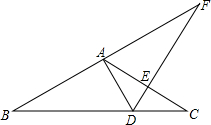 如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线
如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线AC上,直线DE交直线BA于点F,且∠BDA=∠CDE
(1)求证:BF•CE=AB2;
(2)当∠BAC=120°时,作射线CF,在射线CF上确定一点G,使∠BGC=∠ABC,直线BG交直线AC于H,请你猜想AB,CE,AH这三条线段之间的数量关系,并且证明你的猜想.
考点:相似三角形的判定与性质,全等三角形的判定与性质,含30度角的直角三角形,平行线分线段成比例
专题:分类讨论
分析:(1)如图1,作辅助线;证明
=
;证明
=
;证明
=
,得到
=
,得到BF×CE=AB2.
(2)如图2或3,作辅助线;证明BC2=CH×BF;证明BC2=3AB2,得到CH×BF=3BF×CE,得到CH=3CE,即可解决问题.
| AB |
| BF |
| BK |
| BD |
| CE |
| AC |
| CD |
| CK |
| BK |
| BD |
| CD |
| CK |
| AB |
| BF |
| CE |
| AC |
(2)如图2或3,作辅助线;证明BC2=CH×BF;证明BC2=3AB2,得到CH×BF=3BF×CE,得到CH=3CE,即可解决问题.
解答: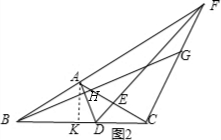
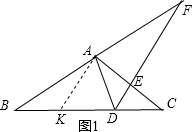
解:(1)如图1,过A作DF的平行线交BC于K,
∵AK∥DF,
∴
=
;
∵AK∥DE,
∴
=
;
∵∠BDA=∠CDE,
∴∠AKC=∠ADB;
∵AB=AC,
∴∠B=∠C,在△ABD与△ACK中,
,
∴△ABD≌△ACK(AAS),
∴BD=CK,BK=CD,
∴
=
,
∴
=
,
∴BF•CE=AB•AC,而AB=AC,
∴BF×CE=AB2.
(2)∵∠BGC=∠BCH,∠GBC=∠CBH,
∴△GBC∽△CBH,
∴∠BHC=∠BCG;
∵∠FBC=∠HCB,
∴△BHC∽△FCB,
∴
=
,
∴BC2=CH×BF;
过点A作BC的垂线,垂足是K;
∵∠BAC=120°,
∴∠B=∠ACB=30°,BK=CK=
BC;
∵∠AKB=90°,
∴cos∠ABK=
=
,
∴BC2=3AB2,由(1)得BF×CE=AB2,
∴CH×BF=3BF×CE
∴CH=3CE.
①如图2,当H在AC上时,
AB、CE、AH这三条线段之间的数量关系:3CE+AH=AB.
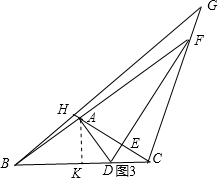
②如图3,当H在CA延长线上时,
AB、CE、AH这三条线段之间的数量关系:3CE-AH=AB.


解:(1)如图1,过A作DF的平行线交BC于K,
∵AK∥DF,
∴
| AB |
| BF |
| BK |
| BD |
∵AK∥DE,
∴
| CE |
| AC |
| CD |
| CK |
∵∠BDA=∠CDE,
∴∠AKC=∠ADB;
∵AB=AC,
∴∠B=∠C,在△ABD与△ACK中,
|
∴△ABD≌△ACK(AAS),
∴BD=CK,BK=CD,
∴
| BK |
| BD |
| CD |
| CK |
∴
| AB |
| BF |
| CE |
| AC |
∴BF•CE=AB•AC,而AB=AC,
∴BF×CE=AB2.
(2)∵∠BGC=∠BCH,∠GBC=∠CBH,
∴△GBC∽△CBH,
∴∠BHC=∠BCG;
∵∠FBC=∠HCB,
∴△BHC∽△FCB,
∴
| CH |
| BC |
| BC |
| BF |
∴BC2=CH×BF;
过点A作BC的垂线,垂足是K;
∵∠BAC=120°,
∴∠B=∠ACB=30°,BK=CK=
| 1 |
| 2 |
∵∠AKB=90°,
∴cos∠ABK=
| BK |
| AB |
| ||
| 2 |
∴BC2=3AB2,由(1)得BF×CE=AB2,
∴CH×BF=3BF×CE
∴CH=3CE.
①如图2,当H在AC上时,
AB、CE、AH这三条线段之间的数量关系:3CE+AH=AB.
②如图3,当H在CA延长线上时,
AB、CE、AH这三条线段之间的数量关系:3CE-AH=AB.

点评:该题以三角形为载体,主要考查了全等三角形的判定及其性质的应用、相似三角形的判定及其性质的应用等几何知识点问题;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
经专家估算,南海内的油气资源约合15000亿美元,用科学记数法表示数字15000是( )
| A、15×103 |
| B、1.5×104 |
| C、1.5×103 |
| D、1.5×105 |
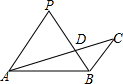 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的( )


| A、①② | B、③② | C、①④ | D、③④ |
 已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E.
已知:如图,在△ABC中,AB=AC=8cm,BC=6cm,AD平分∠BAC,CE⊥AB交AB于E. 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于
如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于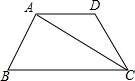 在梯形ABCD中,AD∥BC,AB=AD=DC,∠B=∠BCD=60°,连接AC.求cos∠ACB的值.
在梯形ABCD中,AD∥BC,AB=AD=DC,∠B=∠BCD=60°,连接AC.求cos∠ACB的值.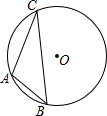 如图,⊙O为△ABC的外接圆,
如图,⊙O为△ABC的外接圆,