题目内容
1．若三角形三个内角的比为1：3：5，则三角形三个内角分别是（ ）| A． | 20°50°110° | B． | 30°60°90° | C． | 20°80°80° | D． | 20°60°100° |
分析 根据三角形内角和定理得出∠A+∠B+∠C=180°，求出即可．
解答 解：如图：
∵∠A+∠B+∠C=180°，∠B：∠C：∠A=1：3：5，
∴∠A=$\frac{5}{9}$×180°=100°，∠B=$\frac{1}{9}$×180°=20°，∠C=$\frac{3}{9}$×180°=60°．
故选D．
点评 本题考查了三角形内角和定理的应用，能熟记三角形内角和定理是解此题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12．设2+$\sqrt{3}$的整数部分用a表示，小数部分用b表示，4-$\sqrt{3}$的整数部分用c表示，小数部分用d表示，则$\frac{b+d}{ac}$的值为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{6}$ | C． | $\frac{5}{6}$ | D． | $\frac{1}{3}$（$\sqrt{3}$-1） |
如图，△ABC为正三角形，点B、C、D、E在同一直线上，且CG=CD=DF=DE，则∠E=15°．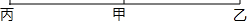
甲、乙、丙三地位置如图所示，甲、乙两地相距30km，丙地离甲地足够远，小明骑自行车从甲地往丙地，小军骑自行车从乙地往丙地，小明的速度为5km/h，小军的速度为15km/h．问：两人同时出发多长时间后相距20km？