题目内容
13.若$sinα=\frac{{\sqrt{6}}}{4}$,则cosα=$\frac{\sqrt{10}}{4}$,tanα=$\frac{\sqrt{15}}{5}$,cos(90°-α)=$\frac{\sqrt{6}}{4}$.分析 sin2α+cos2α=1,tanα=$\frac{sinα}{cosα}$,cos(90°-α)=sinα,根据以上内容求出每个式子即可.
解答 解:∵sin2α+cos2α=1,sinα=$\frac{\sqrt{6}}{4}$,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\sqrt{1-(\frac{\sqrt{6}}{4})^{2}}$=$\frac{\sqrt{10}}{4}$,
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{\sqrt{6}}{4}}{\frac{\sqrt{10}}{4}}$=$\frac{\sqrt{15}}{5}$,
cos(90°-α)=sinα=$\frac{\sqrt{6}}{4}$,
故答案为:$\frac{{\sqrt{10}}}{4}$,$\frac{{\sqrt{15}}}{5}$,$\frac{{\sqrt{6}}}{4}$.
点评 本题考查了同角三角函数的关系,互余两角三角函数的关系的应用,能熟记知识点是解此题的关键.

练习册系列答案
相关题目
4.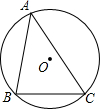 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
1.若三角形三个内角的比为1:3:5,则三角形三个内角分别是( )
| A. | 20°50°110° | B. | 30°60°90° | C. | 20°80°80° | D. | 20°60°100° |
5.下列方程中,解是x=2的是( )
| A. | x+4=2 | B. | 2x-3=2 | C. | x-3=-1 | D. | $\frac{1}{2}$x+1=3 |
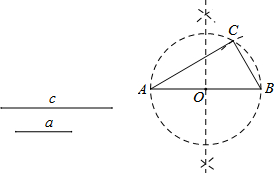 阅读下面材料:
阅读下面材料: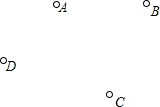 已知平面上有四个点,按要求画图:
已知平面上有四个点,按要求画图: