题目内容
9. 如图,△ABC为正三角形,点B、C、D、E在同一直线上,且CG=CD=DF=DE,则∠E=15°.
如图,△ABC为正三角形,点B、C、D、E在同一直线上,且CG=CD=DF=DE,则∠E=15°.
分析 根据等边三角形三个角相等,可知∠ACB=60°,根据等腰三角形底角相等即可得出∠E的度数.
解答 解:∵△ABC是等边三角形,
∴∠ACB=60°,∠ACD=120°,
∵CG=CD,
∴∠CDG=30°,∠FDE=150°,
∵DF=DE,
∴∠E=15°.
故答案为:15.
点评 本题主要考查了等边三角形的性质,关键是根据互补两角和为180°以及等腰三角形的性质.

练习册系列答案
相关题目
19.把10cm长的线段进行黄金分割,则较长线段的长($\sqrt{5}$≈2.236,精确到0.01)是( )
| A. | 3.09cm | B. | 3.82cm | C. | 6.18cm | D. | 7.00cm |
4.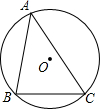 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
1.若三角形三个内角的比为1:3:5,则三角形三个内角分别是( )
| A. | 20°50°110° | B. | 30°60°90° | C. | 20°80°80° | D. | 20°60°100° |
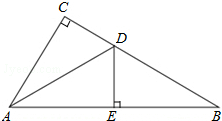 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E. 画出函数y=-3x+2的图象.
画出函数y=-3x+2的图象.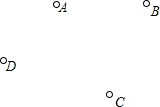 已知平面上有四个点,按要求画图:
已知平面上有四个点,按要求画图: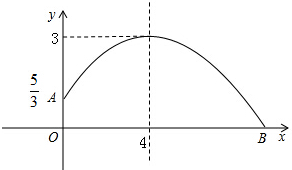 小亮推铅球时,铅球行进高度y(m)与水平距离x(m)之间的关系如图所示(二次函数图象的一部分).
小亮推铅球时,铅球行进高度y(m)与水平距离x(m)之间的关系如图所示(二次函数图象的一部分).