题目内容
12.设2+$\sqrt{3}$的整数部分用a表示,小数部分用b表示,4-$\sqrt{3}$的整数部分用c表示,小数部分用d表示,则$\frac{b+d}{ac}$的值为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$($\sqrt{3}$-1) |
分析 由1<3<4,可知1<$\sqrt{3}$<2,然后可求得a、b的值,最后代入计算即可.
解答 解:∵1<3<4,
∴1<$\sqrt{3}$<2.
∴a=3,b=$\sqrt{3}-1$,c=2,d=2-$\sqrt{3}$.
∴b+d=1,ac=6.
∴$\frac{b+d}{ac}$=$\frac{1}{6}$.
故选:B.
点评 本题主要考查的是估算无理数的大小,求得a=3,b=$\sqrt{3}-1$,c=2,d=2-$\sqrt{3}$是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列图形中,轴对称图形的个数为( )


| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
4.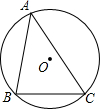 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
1.若三角形三个内角的比为1:3:5,则三角形三个内角分别是( )
| A. | 20°50°110° | B. | 30°60°90° | C. | 20°80°80° | D. | 20°60°100° |
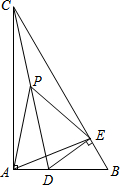 如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.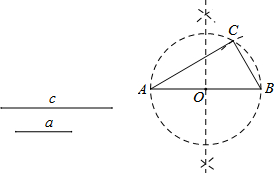 阅读下面材料:
阅读下面材料: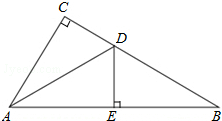 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.