题目内容
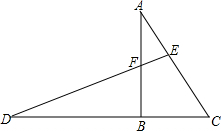 如图,已知:在△ABC中,∠ABC=90°,AB=4,BC=2,将△ABC绕点B逆时针旋转得到△DBF,延长D交AC于点E.
如图,已知:在△ABC中,∠ABC=90°,AB=4,BC=2,将△ABC绕点B逆时针旋转得到△DBF,延长D交AC于点E.(1)求证:DE⊥AC;
(2)求证:DF•DE=DB•DC;
(3)求sin∠EDC的值和AE,EF的长.
考点:相似三角形的判定与性质
专题:
分析:(1)易证∠AFE=∠C,根据∠C+∠A=90°,可得∠AFE+∠A=90°,即可解题;
(2)易证△DBF∽△DEC,可得
=
,即可解题;
(3)易求得AC的长,即可求得sinA的值,根据∠EDC=∠A即可求得sin∠EDC的值,易求得AF的长,即可解题.
(2)易证△DBF∽△DEC,可得
| DF |
| DC |
| DB |
| DE |
(3)易求得AC的长,即可求得sinA的值,根据∠EDC=∠A即可求得sin∠EDC的值,易求得AF的长,即可解题.
解答:(1)证明:∵∠C=∠BFD,∠BFD=∠AFE,
∴∠AFE=∠C,
∵∠C+∠A=90°,
∴∠AFE+∠A=90°,
∴∠AEF=90°,
∴DE⊥AC;
(2)证明:∵∠D=∠D,∠C=∠BFD,
∴△DBF∽△DEC,
∴
=
,
∴DF•DE=DB•DC;
(3)解:∵AC2=BC2+AB2=20,
∴AC=2
,
∵∠EDC=∠A,
∴sin∠EDC=sinA=
=
,
∵BC=BC=2,AB=4,
∴AF=2,
∴EF=AF•sinA=
,
∵AE2=AF2-EF2,
∴AE=
.
∴∠AFE=∠C,
∵∠C+∠A=90°,
∴∠AFE+∠A=90°,
∴∠AEF=90°,
∴DE⊥AC;
(2)证明:∵∠D=∠D,∠C=∠BFD,
∴△DBF∽△DEC,
∴
| DF |
| DC |
| DB |
| DE |
∴DF•DE=DB•DC;
(3)解:∵AC2=BC2+AB2=20,
∴AC=2
| 5 |
∵∠EDC=∠A,
∴sin∠EDC=sinA=
| BC |
| AC |
| ||
| 5 |
∵BC=BC=2,AB=4,
∴AF=2,
∴EF=AF•sinA=
2
| ||
| 5 |
∵AE2=AF2-EF2,
∴AE=
4
| ||
| 5 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,考查了直角三角形中三角函数的运用,考查了直角三角形中勾股定理的运用,本题中求证△DBF∽△DEC是解题的关键.

练习册系列答案
相关题目
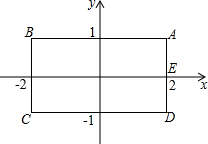 如图,长方形ABCD的各边平行于x轴或y轴,物体甲和物体乙同时从点E(2,0)出发,沿长方形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后第10次相遇地点的坐标是
如图,长方形ABCD的各边平行于x轴或y轴,物体甲和物体乙同时从点E(2,0)出发,沿长方形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后第10次相遇地点的坐标是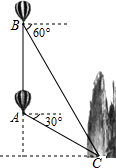 热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据
热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据