题目内容
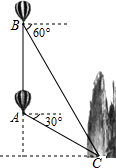 热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据
热气球探测器显示,热气球在点A处看到某小山底部点C的俯角为30°,后垂直上升一定高度至点B,看到点C的俯角为60°,热气球与小山的水平距离为1800米,如图,求热气球垂直上升的高度AB(结果精确到1米,参考数据| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:根据锐角三角函数关系分别得出AD,BD的长,进而求出AB的长.
解答: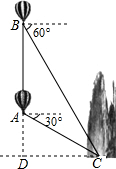 解:过点C作CD⊥BA延长线于点D,
解:过点C作CD⊥BA延长线于点D,
∵热气球与小山的水平距离为1800米,
∴DC=1800m,
∵热气球在点A处看到某小山底部点C的俯角为30°,从点B,看到点C的俯角为60°,
∴∠DBC=30°,∠DAC=60°,
∴tan60°=
=
=
,
∴解得:AD=600
≈1039(m),
tan30°=
=
=
,
解得:BD≈3118(m),
故AB=3118-1039=2079(m),
答:热气球垂直上升的高度AB为2079m.
 解:过点C作CD⊥BA延长线于点D,
解:过点C作CD⊥BA延长线于点D,∵热气球与小山的水平距离为1800米,
∴DC=1800m,
∵热气球在点A处看到某小山底部点C的俯角为30°,从点B,看到点C的俯角为60°,
∴∠DBC=30°,∠DAC=60°,
∴tan60°=
| DC |
| AD |
| 1800 |
| AD |
| 3 |
∴解得:AD=600
| 3 |
tan30°=
| DC |
| BD |
| 1800 |
| BD |
| ||
| 3 |
解得:BD≈3118(m),
故AB=3118-1039=2079(m),
答:热气球垂直上升的高度AB为2079m.
点评:本题主要考查了仰角与俯角的计算,一般三角形的计算,常用的方法是利用作高线转化为直角三角形的计算.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
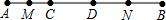 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )| A、7.6cm | B、7.8cm |
| C、8cm | D、8.2cm |
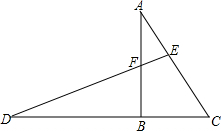 如图,已知:在△ABC中,∠ABC=90°,AB=4,BC=2,将△ABC绕点B逆时针旋转得到△DBF,延长D交AC于点E.
如图,已知:在△ABC中,∠ABC=90°,AB=4,BC=2,将△ABC绕点B逆时针旋转得到△DBF,延长D交AC于点E. 如图所示,线段AB=8cm,C为线段AB上一点,又知M是线段BC的中点,N是线段AC的中点,求MN的长.
如图所示,线段AB=8cm,C为线段AB上一点,又知M是线段BC的中点,N是线段AC的中点,求MN的长.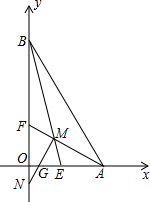 如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.
如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.