题目内容
11.抛物线y=$\frac{1}{2}$(x-1)2-4与x轴的交点坐标为(1+2$\sqrt{2}$,0),(1-2$\sqrt{2}$,0),与y轴的交点坐标为(0,-$\frac{7}{2}$).分析 令y=0,求出x的值,进而抛物线与x轴的交点坐标;求出令x=0求出y的值即可得到与y轴的交点坐标.
解答 解:令y=0,即y=$\frac{1}{2}$(x-1)2-4=0,
解得x1=2$\sqrt{2}$+1,x2=1-2$\sqrt{2}$,
则抛物线与x轴的交点坐标为(1+2$\sqrt{2}$,0),(1-2$\sqrt{2}$,0);
令x=0,y=-$\frac{7}{2}$,
则抛物线与y轴的交点坐标为(0,-$\frac{7}{2}$);
故答案为(1+2$\sqrt{2}$,0),(1-2$\sqrt{2}$,0);(0,-$\frac{7}{2}$).
点评 本题考查了二次函数图象上点的坐标特征,是基础题,掌握抛物线与坐标轴的交点的求法是解题的关键.

练习册系列答案
相关题目
1.用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
| A. | 0.1(精确到0.1) | B. | 0.05(精确到百分位) | ||
| C. | 0.050(精确到0.01) | D. | 0.0502(精确到0.0001) |
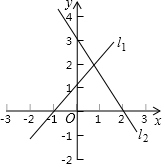 已知:如图所示的坐标系中两直线l1、l2的交点坐标,可以看作哪个方程组的解?
已知:如图所示的坐标系中两直线l1、l2的交点坐标,可以看作哪个方程组的解?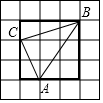 如图,在边长为1的格点图中,求△ABC的周长和面积.
如图,在边长为1的格点图中,求△ABC的周长和面积. 如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3.
如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3.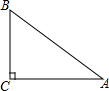 已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km.
已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km.