Question

6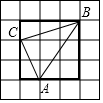．如图，在边长为1的格点图中，求△ABC的周长和面积．

Answer 1

分析 利用勾股定理计算出AC、AB、BC的长，然后可求出周长，再利用矩形的面积减去周围多余三角形的面积可得△ABC面积．

解答 解：BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，
△ABC的周长：$\sqrt{10}$+$\sqrt{5}$+$\sqrt{13}$，
面积：3×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3=9-$\frac{3}{2}$-1-3=3.5．

点评 此题主要考查了勾股定理，关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．