题目内容
9. 如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3.
如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM=3.
分析 过P作PC垂直于MN,由等腰三角形三线合一性质得到MC=CN,求出MC的长,在直角三角形OPC中,利用30度角所对的直角边等于斜边的一半求出OC的长,由OC-MC求出OM的长即可.
解答  解:过P作PC⊥MN,
解:过P作PC⊥MN,
∵PM=PN,
∴C为MN中点,即MC=NC=$\frac{1}{2}$MN=1,
在Rt△OPC中,∠AOB=60°,
∴∠OPC=30°,
∴OC=$\frac{1}{2}$OP=4,
则OM=OC-MC=4-1=3,
故答案为:3
点评 此题考查了含30度角的直角三角形,以及等腰三角形的性质,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
14. 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )| A. | 200m | B. | 20$\sqrt{10}$m | C. | 40$\sqrt{2}$m | D. | 50m |
 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于F,且BF=AC,FD=CD,AD=3,求AB的长. 如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16.
如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16.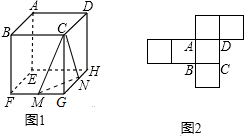 如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段
如图,正方体(图1)的展开图如图2所示,在图1中M、N分别是FG、GH的中点,CM、CN、MN是三条线段;请在图2中画出CM、CN、MN这三条线段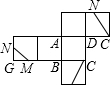 .
.