题目内容
2.王强在电脑上进行高尔夫球的模拟练习,从原点处按函数关系式y=-$\frac{1}{5}$x2+$\frac{8}{5}$x击球,球正好进洞中,y(m)是球的飞行高度,x(m)是求飞出的距离.(1)画出函数y=-$\frac{1}{5}$x2+$\frac{8}{5}$x的图象;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?
分析 (1)将抛物线配方化顶点式,求出的顶点坐标,对称轴,与x轴的交点坐标,画出图象即可.
(2)根据(1)中的图象即可解决问题.
解答 解:(1)∵y=-$\frac{1}{5}$x2+$\frac{8}{5}$x=-$\frac{1}{5}$(x-4)2+$\frac{16}{5}$,
∵-$\frac{1}{5}$<0,
∴开口向下,顶点为(4,$\frac{16}{5}$),对称轴为x=4.
令y=0,则-$\frac{1}{5}$x2+$\frac{8}{5}$x=0,
∴x1=0,x2=8,
∴抛物线与x轴的交点坐标为(0,0)或(8,0).
函数图象如图所示,
(2)由图可知球洞离击球点的距离为:8m.
点评 本题考查的是二次函数在实际生活中的应用,解题的关键是熟练掌握配方法,确定抛物线的顶点坐标,会求抛物线与坐标轴的交点坐标,体现了数形结合的思想,属于中考常考题型.

练习册系列答案
相关题目
14. 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,则A,B两点间的距离是( )| A. | 200m | B. | 20$\sqrt{10}$m | C. | 40$\sqrt{2}$m | D. | 50m |
11.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是( )
| A. | sinA=$\frac{5}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{13}{12}$ | D. | $\frac{1}{tanA}$=$\frac{5}{12}$ |
12.点A、B、C在同一条数轴上,其中点A、B表示的数分别为-3、1,若BC的长为2,则AC的长为( )
| A. | 4 | B. | 2 | C. | 3或5 | D. | 2或6 |
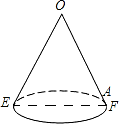 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.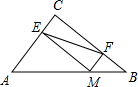 如图,在△ABC中,AC=9,BC=12,AB=15,点M为AB边上的点,过M作ME⊥AC交AC于E,MF⊥BC交BC于F,连接EF,则EF的最小值为$\frac{36}{5}$.
如图,在△ABC中,AC=9,BC=12,AB=15,点M为AB边上的点,过M作ME⊥AC交AC于E,MF⊥BC交BC于F,连接EF,则EF的最小值为$\frac{36}{5}$.