题目内容
2.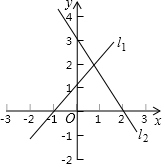 已知:如图所示的坐标系中两直线l1、l2的交点坐标,可以看作哪个方程组的解?
已知:如图所示的坐标系中两直线l1、l2的交点坐标,可以看作哪个方程组的解?
分析 设直线l1的解析式为y=kx+b,直线l2的解析式为y=mx+n,根据图形找出点的坐标利用待定系数法分别求出直线l1、l2的解析式,由此即可交点坐标为方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
解答 解:设直线l1的解析式为y=kx+b,直线l2的解析式为y=mx+n,
将(-1,0)、(0,1)代入y=kx+b中,
$\left\{\begin{array}{l}{-k+b=0}\\{b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线l1的解析式为y=x+1,
将(0,3)、(2,0)代入y=mx+n中,
$\left\{\begin{array}{l}{n=3}\\{2m+n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-\frac{3}{2}}\\{n=3}\end{array}\right.$,
∴直线l2的解析式为y=-$\frac{3}{2}$x+3.
∴两直线的交点坐标为方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
点评 本题考查了待定系数法求一次函数解析式以及一次函数与二元一次方程组,根据图形中点的坐标利用待定系数法分别求出直线l1、l2的解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.20142-2013×2015的计算结果是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
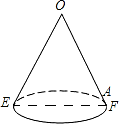 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$. 如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16.
如图,已知∠AOB=30°,点P在边OA上,点M、N在边OB上,且PM=PN=10,MN=12,则OP=16.