题目内容
6．
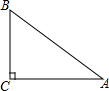已知A，B，C三地位置如图所示，∠C=90°，A，C两地的距离是4km，B，C两地的距离是3km，则A，B两地的距离是5km．
分析 在直角三角形ABC中，∠C=90°，然后又知道两直角边的长，再根据勾股定理的性质即可求得斜边的长．
解答 解：∵直角三角形ABC，∠C=90°，AC=4km，BC=3km，
∴AB2=AC2+BC2，即AB=$\sqrt{{4}^{2}+{3}^{2}}$=5km，
∴A，B两地的距离为5km，
故答案为：5．
点评 本题主要考查了勾股定理的应用，键是从题中抽象出勾股定理这一数学模型，画出准确的示意图，领会数形结合的思想的应用．
练习册系列答案
相关题目
10．20142-2013×2015的计算结果是（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
14．
如图，池塘边有两点A、B，点C是与BA方向成直角的AC方向上一点，测得CB=60m，AC=20m，则A，B两点间的距离是（ ）
如图，池塘边有两点A、B，点C是与BA方向成直角的AC方向上一点，测得CB=60m，AC=20m，则A，B两点间的距离是（ ）| A． | 200m | B． | 20$\sqrt{10}$m | C． | 40$\sqrt{2}$m | D． | 50m |
11．Rt△ABC中，∠C为直角，AC=5，BC=12，那么下列∠A的四个三角函数中正确的是（ ）
| A． | sinA=$\frac{5}{13}$ | B． | cosA=$\frac{12}{13}$ | C． | tanA=$\frac{13}{12}$ | D． | $\frac{1}{tanA}$=$\frac{5}{12}$ |
如图，已知∠AOB=30°，点P在边OA上，点M、N在边OB上，且PM=PN=10，MN=12，则OP=16．
15．下列语句正确的是（ ）
| A． | “+15米”表示向东走15米 | |
| B． | 0℃表示没有温度 | |
| C． | 在一个正数前添上一个负号，它就成了负数 | |
| D． | 0 既是正数也是负数 |