题目内容
17.在平面直角坐标系xOy中,给出如下定义:对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
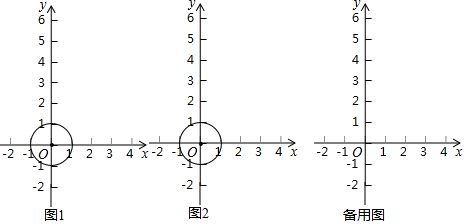
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;
若点P在直线x=2上,则点P关于⊙O的最大“视角”的度数60°;
②在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标.
(2)若点P在直线y=-$\frac{\sqrt{3}}{3}$x+2上,且点P关于⊙O的“视角”大于60°,求点P的横坐标xP的取值范围.
(3)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,-1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标xC的取值范围.
分析 (1)①由定义可知即可画出图形:当∠MPN最大时,此时点P关于⊙O的视角,此时PM与PN与⊙O相切,从而可求出视角的度数;
②由①可知:B关于⊙O的“视角”为60°,此时OB=2,根据勾股定理即列出方程即可求出m的值;
(2)点P关于⊙O的“视角”大于60°,所以点P在以O为圆心,1为半径与2为半径的圆环内.
(3)分点C在x轴正半轴和负半轴两种情况讨论计算即可.
解答 解:(1)①画如图1所示,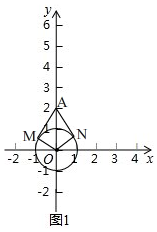
如图2,当∠MPN最大时,此时PM与PN与⊙O相切,
∵⊙O的半径为r=1,
∴sin∠MPO=$\frac{OM}{OP}$,
当OP最小时,此时sin∠MPO最大,即∠MPO最大,
∴sin∠MPO=$\frac{1}{2}$,
∴∠MPO=30°
∴∠MPN=2∠MPO=60°;
故答案为:60°
②∵点B关于⊙O的视角为60°,
∴BM与⊙O相切,且∠MBO=30°,
∴点B在以O为圆心,2为半径的圆上,即OB=2,
∵B(m,m) (m>0),
∴OB=$\sqrt{{m}^{2}+{m}^{2}}$=$\sqrt{2}$m=2,
∴m=$\sqrt{2}$
∴B($\sqrt{2}$,$\sqrt{2}$);
(2)如图3,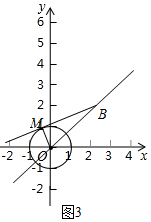
∵点P关于⊙O的“视角”大于60°,
∴∠MPO>30°,
∴sin∠MPO=$\frac{1}{OP}$>sin30°,
∴OP<2,
∵点P不在⊙C上,
∴1<OP<2
∴点P在以O为圆心,1为半径与2为半径的圆环内,
∵点P在直线y=$-\frac{\sqrt{3}}{3}$x+2上,
由图4,
可得xp=0或xP=$\sqrt{3}$
∴0<xP<$\sqrt{3}$
(3)如图5,
①当点C在x轴正半轴时,
在线段EF上取一点P,当PM,PN都与⊙C相切时,∠MPN最大,当∠MPN=120°时,连接CP,
∴∠CPM=60°,
在Rt△PCM中,CM=1,sin∠CPM=$\frac{CM}{CP}$=$\frac{1}{CP}$=$\frac{\sqrt{3}}{2}$,
∴CP=$\frac{2\sqrt{3}}{3}$,
∵线段EF上所有的点关于⊙C的“视角”都小于120°,
∴点P和原点O重合时,视角只要小于120°时,即可,OP最大=CP=$\frac{2\sqrt{3}}{3}$,
此时,满足条件的xC$>\frac{2\sqrt{3}}{3}$
②当点C在x轴负半轴时,同①可得,xC<-$\frac{2\sqrt{3}}{3}$,
即:满足条件的xC$>\frac{2\sqrt{3}}{3}$或xC<-$\frac{2\sqrt{3}}{3}$.
点评 此题是圆的综合题,主要考查了圆的切线的性质,勾股定理,锐角三角函数,“视角”的定义的理解,解(1)的关键是判断出PM,PN与⊙O相切时,“视角”最大,解(2)(3)的关键是确定出分界点的坐标,是一道中等难度的题目.

| A. |  | B. |  | C. |  | D. |  |
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
| A | B | |
| 成本(万元/件) | 100 | 80 |
| 售价(万元/件) | 170 | 120 |
(1)写出y与x的函数关系式;
(2)如果该服装店平均每月投入的总成本不超过7500元,不考虑其他因素,那么当A、B两种品牌服装各销售多少件时,该服装店平均每月的总利润最大?并求出这个最大利润.
| A. | 有最大值$\frac{a}{4}$ | B. | 有最大值-$\frac{a}{4}$ | C. | 有最小值$\frac{a}{4}$ | D. | 有最小值-$\frac{a}{4}$ |
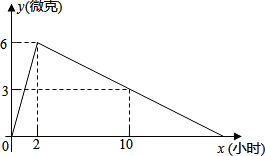 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,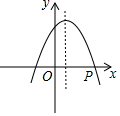 如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.