��Ŀ����
5��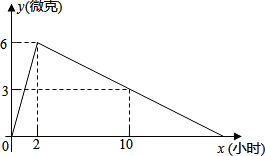 ijҽҩ�о���������һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱʱѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�������˥����10СʱѪҺ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y����ʱ��xСʱ���仯��ͼ��ʾ�������˰��涨���Ƿ�ҩ��
ijҽҩ�о���������һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱʱѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�������˥����10СʱѪҺ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y����ʱ��xСʱ���仯��ͼ��ʾ�������˰��涨���Ƿ�ҩ����1���ֱ����x��2��x��2ʱy��x�ĺ�����ϵʽ��
��2�����ÿ����ѪҺ�к�ҩ��Ϊ4�˻�4������ʱ�����Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ��
���� ��1��ֱ�Ӹ���ͼ���ϵĵ���������ô���ϵ������ã�
��2������ͼ���֪ÿ����ѪҺ�к�ҩ��Ϊ4��������������ͼ���϶��У�����y=4���ֱ����y=3x��y=-$\frac{3}{8}$x+$\frac{27}{4}$�����x��ֵ���ɽ�����⣻
��� �⣺��1����x��2ʱ����y=k1x��
�ѣ�2��6��������ʽ����k1=3��
��x��2ʱ��y=3x��
��x��2ʱ����y=k2x+b��
�ѣ�2��6������10��3��������ʽ��$\left\{\begin{array}{l}{2{k}_{2}+b=6}\\{10{k}_{2}+b=3}\end{array}\right.$
��k2=-$\frac{3}{8}$��b=$\frac{27}{4}$��
��x��2ʱ��y=-$\frac{3}{8}$x+$\frac{27}{4}$��
��2����y=4����y=3x����x1=$\frac{4}{3}$��
��y=4����y=-$\frac{3}{8}$x+$\frac{27}{4}$����x2=$\frac{22}{3}$��
��x2-x1=6Сʱ��
�������Чʱ��Ϊ6Сʱ��
���� ������Ҫ��������һ�κ�����ģ�ͽ��ʵ������������Ͷ�ͼ������Ҫ�ȸ��������г�������ϵʽ���ٴ�����ֵ������Ĺؼ���Ҫ�����������ʵ������ȷ���г�����ʽ���ٰѶ�Ӧֵ������⣬�������ͼʾ�ó�����Ҫ����Ϣ��

 ��ͼ����ACD=120�㣬��B=20�㣬���A�Ķ����ǣ�������
��ͼ����ACD=120�㣬��B=20�㣬���A�Ķ����ǣ�������| A�� | 120�� | B�� | 90�� | C�� | 100�� | D�� | 30�� |
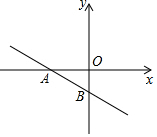 ��ͼ��һ�κ���y=ax+b��ͼ��ֱ���x�ᡢy��ĸ������ཻ��A��B�������н���һ����ȷ���ǣ�������
��ͼ��һ�κ���y=ax+b��ͼ��ֱ���x�ᡢy��ĸ������ཻ��A��B�������н���һ����ȷ���ǣ�������| A�� | a-b��0 | B�� | a+b��0 | C�� | b-a��0 | D�� | -a-b��0 |
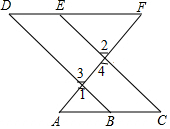 ��ͼ����B��AC�ϣ���E��D��F���㹲�ߣ���2=��1����FEC=��DBA����֤��AC��DF�Ĺ��̲���������
��ͼ����B��AC�ϣ���E��D��F���㹲�ߣ���2=��1����FEC=��DBA����֤��AC��DF�Ĺ��̲���������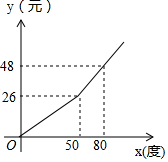 ij���е�ҵ��Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취������Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ�����ϵ��ͼ��ʾ��
ij���е�ҵ��Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취������Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ�����ϵ��ͼ��ʾ��
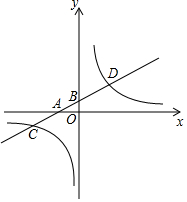 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y1=kx+b��ͼ��ֱ�x�ᣬy����A��B���㣬�뷴��������y2=$\frac{n}{x}$��ͼ����C��D���㣬��֪��C������Ϊ��-4��-1������D�ĺ�����Ϊ2��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y1=kx+b��ͼ��ֱ�x�ᣬy����A��B���㣬�뷴��������y2=$\frac{n}{x}$��ͼ����C��D���㣬��֪��C������Ϊ��-4��-1������D�ĺ�����Ϊ2��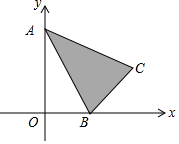 ��ͼ����֪��ABC�Ķ�������ֱ�ΪA��0��2����B��1��0����C��2��1���������κ���y=x2+bx+1��ͼ������Ӱ���֣����߽磩һ���й����㣬��ʵ��b��ȡֵ��Χ�ǣ�������
��ͼ����֪��ABC�Ķ�������ֱ�ΪA��0��2����B��1��0����C��2��1���������κ���y=x2+bx+1��ͼ������Ӱ���֣����߽磩һ���й����㣬��ʵ��b��ȡֵ��Χ�ǣ�������