题目内容
12.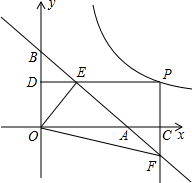 如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F
如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F(1)用含b的代数式表示E点的坐标(1-b,b)
用含a的代数式表示F点的坐标(a,1-a)
(2)求证:△AOE∽△BFO
(3)当点P在双曲线y=$\frac{1}{2x}$(x>0)上移动时,∠EOF也随之变化,试问∠EOF的大小是否变化,如果不变,求出其值,如果变化,说明理由.
分析 (1)易得点E的纵坐标为b,点F的横坐标为a,代入直线的解析式y=-x+1,即可用a,b的式子表示出E、F两点的坐标;
(2)由直线y=-x+1与x,y轴分别交于A、B两点可得OA=OB=1,从而得到∠OAB=45°,将OE2、EF、EA分别用a、b的代数式表示,可得OE2=EF•EA,可证明△EOF∽△EAO,可得到∠EOA=∠EFO,又∠EAO=∠FBO,可证明△AOE∽△BFO;
(3)由(2)可得∠EOF=∠OAE=45°,其值不变.
解答 解:(1)如图1,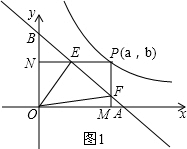
∵PM⊥x轴与M,交线段AB于F,
∴xF=xM=xP=a,
∵PN⊥y轴于N,交线段AB于E,
∴yE=yN=yP=b,
∵点E、F在直线AB上,
∴yE=-xE+1=b,yF=-xF+1=-a+1,
∴xE=1-b,yF=1-a,
∴点E的坐标为(1-b,b),点F的坐标为(a,1-a).
故答案为:(1-b,b);(a,1-a);
(2)证明:
过点E作EH⊥OM,垂足为H,如图2,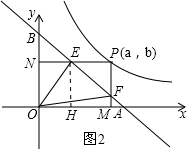
∵EN⊥ON,
∴OE2=ON2+EN2=b2+(1-b)2=2b2+1-2b,
∵EH⊥OM,EH=b,AH=1-(1-b)=b,
∴EA=$\sqrt{{b}^{2}+{b}^{2}}$=$\sqrt{2}$b,
同理可得:FA=$\sqrt{2}$(1-a),
∴EF=EA-FA=$\sqrt{2}$b-$\sqrt{2}$(1-a)=$\sqrt{2}$(b+a-1),
∵2ab=1,
∴EF•EA=$\sqrt{2}$(b+a-1)$\sqrt{2}$b=2(b2+ab-b)=2b2+2ab-2b=2b2+1-2b,
∴OE2=EF•EA,
∴$\frac{OE}{EF}$=$\frac{EA}{OE}$,
∵∠OEF=∠AEO,
∴△OEF∽△AEO,
∴∠EFO=∠AOE,
∵OA=OB=1,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∴△AOE∽△BFO;
(3)由(2)可知△OEF∽△AEO,
∴∠EOF=∠EAO=45°,
∴∠EOF的大小不变,始终等于45°.
点评 本题为反比例函数的综合应用,涉及知识点有矩形的判定与性质、相似三角形的判定与性质、反比例函数图象上点的坐标特征、勾股定理、完全平方公式等.在(2)中证得△OEF∽△AEO是解题的关键,为(3)的解决提供了条件.本题考查知识点较多,综合性很强,特别是第(2)问难度很大.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | (2,4) | B. | (-1,2) | C. | (5,1) | D. | (-1,-4) |

若整数2016位于第a行,从左数第b个数,则a+b的值是( )
| A. | 63 | B. | 126 | C. | 2015 | D. | 1002 |
| A. | a•a2=a3 | B. | 3a+2a2=5a2 | C. | 2-3=-8 | D. | $\sqrt{9}$=±3 |
| 成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.70,9.60 | B. | 9.60,9.60 | C. | 9.60,9.70 | D. | 9.65,9.60 |
 现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.
现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.