题目内容

8．如果四边形内的一个点到四条边的距离相等，那么这个四边形一定有（　　）
A．一组邻边相等B．一组对边平行
C．两组对边分别相等D．两组对边的和相等

分析 由四边形内的一个点到四条边的距离相等，可得出该四边形为圆外切四边形，画出图形，根据切线的性质即可得出各组相等的线段，根据线段间的关系即可得出结论．

解答 解：依照题意，画出图形，如图所示．

∵如果四边形内的一个点到四条边的距离相等，
∴四边形ABCD为⊙O的外切四边形，
∴AE=AN，DN=DM，CM=CF，BF=BE，
∵AD=AN+DN，BC=BF+CF，AB=AE+BE，CD=CM+DM，
∴AD+BC=AB+CD．
故选D．

点评 本题考查了角平分线的性质以及切线的性质，解题的关键是得出该四边形为圆外切四边形．本题属于中档题，难度不大，解决该题型题目时，根据角平分线的性质确定该四边形为圆外切四边形是关键．

练习册系列答案
相关题目
6．如图，点A为y轴正半轴上一点，点B是A关于x轴的对称点，过点A任意作一条直线，与抛物线y=$\frac{3}{4}$x2交于P，Q两点．

（1）如图1，若PQ∥x轴，点A坐标为（0，3），求证：∠ABP=∠ABQ
（2）若直线绕点A旋转到图2的位置，问：题（1）中的结论是否依然成立，请说明理由．
7．下列运算正确的是（　　）
A．a•a2=a3B．3a+2a2=5a2C．2-3=-8D．$\sqrt{9}$=±3
4．不等式组$\left\{\begin{array}{l}{3（x+1）＞x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$的整数解的和是（　　）
A．-1B．1C．0D．1
3．在矩形ABCD上有一个动点P，点P沿AD-DC-CA运动，并且不与点A重合，连接BP，以BP为直角边作等腰直角三角形BPQ，AB=6，AD=4．

（1）当点P沿AD-DC-CA运动时，求出等腰直角三角形BPQ面积的最大值；
（2）当点P在AD上运动时，△BPQ的边PQ与DC交于点E，如图1所示，若AP：AD=1：2时，AB：PD的值为3；若AP：AD=1：n时，AB：PD的值为$\frac{3n}{2（n-1）}$；
（3）如图2所示，当点P（不与点D、C重合）在DC上运动时，请你判断梯形ABPD的面积是否可为△BPQ面积的4倍？若可以，请求出PC的长度；若不可以，请说明理由；
（4）如图3所示，当点P运动到CA的延长线上时，请你直接写出BP：PF的值．
13．在△ABC中，AD是△ABC的高，若AB=$\sqrt{6}$，tan∠B=$\frac{\sqrt{2}}{2}$，且BD=2CD，则BC=3或1．
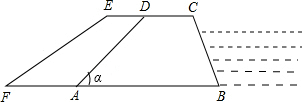20．如图，某堤坝的横截面是梯形ABCD，背水坡AD的坡度（即tanα）为1：1.2，坝高10米，为了提高坝的防洪能力，由相关部门决定加固堤坝，要求将坝顶CD加宽2米，形成新的背水坡EF，其坡度为1：1.4，已知堤坝总长度为1000米．
（1）求完成该工程需要多少土方？
（2）该工程由甲、乙两工程队同时合作完成，按计划需20天，准备开工前接到上级要求，汛期可能提前，要求两工程队提高工作效率，甲队工作效率提高30%，乙队工作效率提高40%，结果提前5天完成．问这两个工程队原计划每天各完成多少土方？
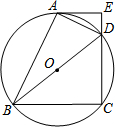17．如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE交CD的延长线于点E，DA平分∠BDE．
（1）求证：AE⊥CD；
（2）已知AE=4cm，CD=6cm，求⊙O的半径．
18．因式分解：（a+b）2-4b2=（a+3b）（a-b）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网