��Ŀ����
15���ڡ�ABC�У���ACB=90�㣬CD��AB�ڵ�D����1����ͼ��1����AC=BC����E��F�ֱ���AC��BC�ϣ���EDF=90�㣬��DE��DF��������ϵΪDE=DF��
��2����ͼ��2����AC=BC���ӳ�BC����F����CA����ƽ���߶�CF��EG���ҵ�G�ڱ�BA���ӳ����ϣ���֤��DE=DF��DE��DF��
��3����ͼ��3������B=30�㣬�ӳ�BC����F����CA����ƽ���߶�CF��EG���ҵ�G�ڱ�BA���ӳ����ϣ�ֱ��д���߶�DE��DF��λ�ù�ϵ��������ϵ��
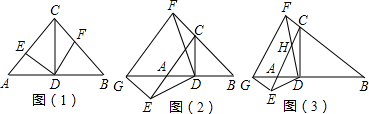
���� ��1����֤��DE=DF��ֻҪ֤����ADE�ա�CDF���ɣ�
��2����֤��DE=DF��DE��DF��ֻҪ֤����ADE�ա�CDF��
��3����֤��DF=$\sqrt{3}$DE��DE��DF��ֻҪ֤����DCF�ס�DAE���Ʊ���$\sqrt{3}$���ɣ�
��� ��1��֤������ͼ��1���У�
��CA=CB����ACB=90�㣬CD��AB��
���A=��B=��ACD=��BCD=45�㣬AD=DC=DB��
�ߡ�ADC=��EDF=90�㣬
���ADE=��CDF��
�ڡ�ADE�͡�CDF�У�
$\left\{\begin{array}{l}{��A=��DCF}\\{AD=CD}\\{��ADE=��CDF}\end{array}\right.$��
���ADE�ա�CDF��
��DE=DF��
�ʴ�ΪDE=DF��
��2��֤������ͼ��2���У�
��CF=GE��CF��EG��
���ı���CEGF��ƽ���ı��Σ�
��CE��FG��
���CAB=��FGA=45��
�ߡ�ECF=��ACB=90�㣬
���ı���CEGF�Ǿ��Σ�
���GEA=��FGE=90�㣬
���AGF=��GAF=45�㣬
��GE=AE=CF��
��CD=DA=DB����DCB=��GAE=45�㣬
���FCD=��DAE=135�㣬
�ڡ�DAE�͡�DCF�У�
$\left\{\begin{array}{l}{DC=DA}\\{��FCD=��EAD}\\{CF=AE}\end{array}\right.$��
���DCF�ա�DAE��
��DE=DF����EDA=��FDC��
���EDF=��ADC=90�㣬
��DE��DF��
��3�����ۣ�DF=$\sqrt{3}$DE��DE��DF��
���ɣ���ͼ��3���У�
�ɣ�2����֪�ı���CEGF�Ǿ��Σ�
���GEA=90�㣬
�ߡ�B=30�㣬CD��AB��
���DCB=60�㣬��FCD=120�㣬��CAB=��GAE=60�㣬
���EAD=120�㣬
���FCD=��EAD��
��CD=$\sqrt{3}AD$��EG=CF=$\sqrt{3}$AE��
��CD$\frac{CD}{AD}=\frac{CF}{AE}=\sqrt{3}$��
���DCF�ס�DAE��
��$\frac{DF}{DE}=\frac{DC}{AD}=\sqrt{3}$����FCD=��EDA��
���EDF=��ADC=90�㣬
��DF=$\sqrt{3}$DE��DF��DE��
���� ���⿼��ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ����������ε��ж������ʣ�����Ĺؼ�����ȷѰ��ȫ�������λ����������ν�����⣬�����п��������ͣ�

 ��У����ϵ�д�
��У����ϵ�д�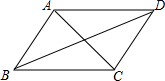 ��ͼ����ƽ���ı���ABCD�У����ӶԽ���AC��BD��ͼ�е�ȫ�������εĶ�����������
��ͼ����ƽ���ı���ABCD�У����ӶԽ���AC��BD��ͼ�е�ȫ�������εĶ�����������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | �ں� | B�� | ���� | C�� | ���� | D�� | �ཻ |
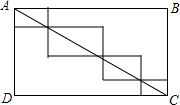 ��ͼ��������ABCD�ı�AB=7��BC=4����ͼ���ĸ�С�����ε��ܳ�֮��Ϊ22��
��ͼ��������ABCD�ı�AB=7��BC=4����ͼ���ĸ�С�����ε��ܳ�֮��Ϊ22��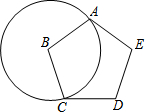 ��ͼ��ʾ���������ABCDE�ı߳�Ϊ1����B������εĶ���A��C�����ӻ�AC�ij�Ϊ$\frac{3}{5}$�У�
��ͼ��ʾ���������ABCDE�ı߳�Ϊ1����B������εĶ���A��C�����ӻ�AC�ij�Ϊ$\frac{3}{5}$�У� С����С���ڹ��ŷ��ݣ���С���÷��ݹ��������ϣ����ݹ̶���A������ͼ����Ϊ������ʱ���ݵĸ߶ȣ����������²��������
С����С���ڹ��ŷ��ݣ���С���÷��ݹ��������ϣ����ݹ̶���A������ͼ����Ϊ������ʱ���ݵĸ߶ȣ����������²��������