题目内容
9．如果a=（-2009）0，b=（-0.1）-1，c=（-$\frac{5}{3}$）-2，那么a、b、c的大小关系为（ ）| A． | a＞b＞c | B． | c＞a＞b | C． | c＞b＞a | D． | a＞c＞b |
分析 根据非零的零次幂等于1，负整数指数幂与正整数指数幂互为倒数，可化简各数，根据有理数的大小比较，可得答案．
解答 解：a=（-2009）0=1，b=（-0.1）-1=-10，c=（-$\frac{5}{3}$）-2=$\frac{9}{25}$，
c＞a＞b，
故选：B．
点评 本题考查了有理数大小比较，利用非零的零次幂等于1，负整数指数幂与正整数指数幂互为倒数化简各数是解题关键．
练习册系列答案
相关题目
19．已知点A、B的坐标分别为（1，0）、（2，0）．若顶点在x轴下方的二次函数y=x2+（a-3）x+3的图象与线段AB恰好只有一个交点，则a的取值范围（ ）
| A． | $-1≤a＜-\frac{1}{2}$ | B． | $-1≤a≤\frac{1}{2}$ | C． | $\frac{1}{2}＜a＜2$ | D． | -1＜a≤1 |
20．下列说法中错误的是（ ）
| A． | 不等式x+1≤4的整数解有无数个 | B． | 不等式x+4＜5的解集是x＜1 | ||
| C． | 不等式x＜4的正整数解为有限个 | D． | 0是不等式3x＜-1的解 |
17．有15张大小、形状及背面完全相同的卡片，卡片正面分别画有正三角形、正方形、圆，从这15张卡片中任意抽取一张正面的图形既是轴对称图形，又是中心对称图形的概率是$\frac{2}{3}$，则正面画有正三角形的卡片张数为（ ）
| A． | 3 | B． | 5 | C． | 10 | D． | 15 |
4．在篮球比赛中，某队员连续10场比赛中每场的得分情况如下所示：
则这10场比赛中该队员得分的中位数和众数分别是（ ）
| 场次（场） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分（分） | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
| A． | 10，4 | B． | 10，13 | C． | 11，4 | D． | 12.5，13 |
14．
已知有理数a、b、c在数轴上的位置如图所示，下列子正确的是（ ）
已知有理数a、b、c在数轴上的位置如图所示，下列子正确的是（ ）| A． | cb＞ab | B． | ac＞ab | C． | cb＜ab | D． | c+b＞a+b |
1．
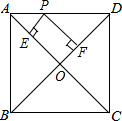如图，在正方形ABCD中，AB=1，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为 （ ）
如图，在正方形ABCD中，AB=1，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为 （ ）| A． | $\sqrt{2}$ | B． | 4 | C． | 2 | D． | $\frac{{\sqrt{2}}}{2}$ |
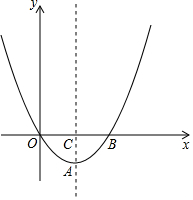如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2-4ax（a≠0）的对称轴交抛物线于A点，交x轴于C点，且AC=OC．