题目内容
3.在△ABC中.(1)△ABC中,∠A=50°,∠C=65°,则∠B=65°,△ABC是直角三角形;
(2)∠A=70°,∠B=∠C,则∠B=55°;
(3)△ABC中,∠C=90°,∠B=2∠A.则∠A=30°.
分析 (1)根据三角形的内角和等于180°求得∠B,进而得到△ABC的形状;
(2)根据三角形的内角和即可得到结论;
(3)根据直角三角形的性质即可得到结论.
解答 解:(1)在△ABC中,∵∠A+∠B+∠C=180°,
∴∠B=180°-∠A-∠C=180°-50°-65°=65°,
∴∠B=∠C,
∴△ABC是等腰三角形.
故答案为:65,直角;
(2)在△ABC中,∵∠A+∠B+∠C=180°,
∴∠B=$\frac{1}{2}$(180°-∠A)=55°.
故答案为:55;
(3)在△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∵∠B=2∠A,
∴∠A=30°.
故答案为:30°.
点评 本题考查了三角形的内角和,等腰三角形的判定,直角三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
12.写出满足如表条件的一次函数表达式为y=-3x+1.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 1 | -2 | -5 |
 如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少?
如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少? 如图,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小.
如图,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小. 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.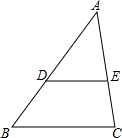 如图,若DE∥BC,CE=$\frac{2}{3}$AE,AB=20,则AD=12.
如图,若DE∥BC,CE=$\frac{2}{3}$AE,AB=20,则AD=12.