题目内容
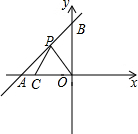 如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).
如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).(1)请写出直线l的解析式;
(2)若点P是直线l上的一个动点,O为坐标原点,
①请写出△OCP的面积S与P的横坐标t的函数关系式;
②探究:当P运动到何处时,△OCP的面积为9?求出此时点P的坐标.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)利用待定系数法即可求得;
(2)①设P点的坐标为(t,
t+6),根据三角形的面积公式即可求得;②把S=9代入①求得的函数关系式即可求得t的值,进而求得P的坐标.
(2)①设P点的坐标为(t,
| 3 |
| 4 |
解答:解:(1)将A(-8,0)代入y=kx+6得:0=-8k+6,解得:k=
,
∴直线l的解析式为y=
x+6.
(2)①∵点P是直线l上的一个动点,
∴设P点的坐标为(t,
t+6),过P作PH⊥x轴于H,则PH=|
t+6|,
∵C(-6,0),
∴OC=6,
∴S=
OC•PH=
×6×|
t+6|=3|
t+6|,
②当S=9时,则S=3|
t+6|=9,
即|
t+6|=3,
∴
t+6=±3,
解得:t1=-4,t2=-12,
∴
×(-4)+6=3,
×(-12)+6=-3.
∴P点的坐标为(-4,3)或(-12,-3).
| 3 |
| 4 |
∴直线l的解析式为y=
| 3 |
| 4 |
(2)①∵点P是直线l上的一个动点,
∴设P点的坐标为(t,
| 3 |
| 4 |
| 3 |
| 4 |
∵C(-6,0),
∴OC=6,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
②当S=9时,则S=3|
| 3 |
| 4 |
即|
| 3 |
| 4 |
∴
| 3 |
| 4 |
解得:t1=-4,t2=-12,
∴
| 3 |
| 4 |
| 3 |
| 4 |
∴P点的坐标为(-4,3)或(-12,-3).
点评:本题考查了待定系数法求解析式,三角形的面积的应用,一次函数图象上点的坐标特点,注意PH=|
t+6|.
| 3 |
| 4 |

练习册系列答案
相关题目
已知点(3-2k2,4k-3)在第一象限的角平分线上,则k=( )
| A、1 | B、-1 | C、0 | D、0或1 |
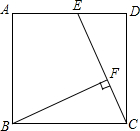 如图,正方形ABCD的边长为4cm,点E为AD的中点,BF⊥EC于点F,求BF的长.
如图,正方形ABCD的边长为4cm,点E为AD的中点,BF⊥EC于点F,求BF的长. 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,BF=FE,DF与AC相交于点M,求证:AM=MC.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,BF=FE,DF与AC相交于点M,求证:AM=MC. 如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.
如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.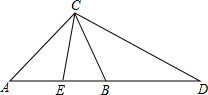 如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.
如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.