题目内容
如图，已知每个小正方形的边长均为1，A、B、C、D是小正方形的顶点，AB、CD交于点O，求∠AOC的度数．考点：勾股定理的逆定理,勾股定理,等腰直角三角形
专题：
分析：根据平行四边形的判定与性质，可得∠AOC=∠DCE，根据勾股定理的逆定理，可得△DEC的形状，根据△DEC的形状，可得答案．
解答：解：连接CE，DE，
，
∵都是小正方形，
∴AC=BE，AC∥BE，
∴四边形ABEC是平行四边形，
∴AB∥CE，
∴∠AOC=∠DCE．
∵DC=
=
，DE=
=
，CE=
=
，
∴DC2+DE2=CE2，DC=DE．
∴△DCE是等腰直角三角形，
∴∠AOC=∠DCE=45°．
，∵都是小正方形，
∴AC=BE，AC∥BE，
∴四边形ABEC是平行四边形，
∴AB∥CE，
∴∠AOC=∠DCE．
∵DC=
| 12+22 |
| 5 |
| 12+22 |
| 5 |
| 12+32 |
| 10 |
∴DC2+DE2=CE2，DC=DE．
∴△DCE是等腰直角三角形，
∴∠AOC=∠DCE=45°．
点评：本题考查了勾股定理的逆定理，利用了平行四边形的判定与性质，勾股定理的逆定理．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
如图所示，将平面图形绕轴旋转一周，得到的几何体是（ ）A、 |
B、 |
C、 |
D、 |
在一直角三角形的两直角边上各取一点，分别沿斜边中线与这两点的连线剪去两个三角形，剩下的部分是如图所示的四边形，其中三边长分别为3、4、4，则原直角三角形的斜边长是（ ）| A、10 | ||
B、8
| ||
C、10或8
| ||
D、10或4
|
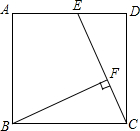如图，正方形ABCD的边长为4cm，点E为AD的中点，BF⊥EC于点F，求BF的长．
如图，在△ABC中，∠ACB=90°，∠BAC=30°，△ABE和△ACD都是等边三角形，BF=FE，DF与AC相交于点M，求证：AM=MC．