题目内容
9.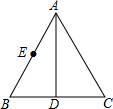 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.
分析 连接CE,则CE的长度即为ME与MB和的最小值,那么CE+BE的和就是△BEM的周长的最小值.
解答 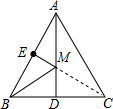 解:如图,连接CE,与AD交于点M,此时ME+MB最小,
解:如图,连接CE,与AD交于点M,此时ME+MB最小,
∵△ABC是等边三角形,AD是等边△ABC的角平分线,
∴AD⊥BC,BD=CD,
∴MC=MB,
∴ME+MB=MC+ME=CE,
即CE就是ME+MB的最小值,
∵AD=6,BD=2$\sqrt{3}$,
∴AB=BC=2BD=4$\sqrt{3}$
∵点E是边AB的中点,
∴∠BEC=90°,BE=2$\sqrt{3}$,BE=AD=6,
∴△BEM的周长的最小值是6+2$\sqrt{3}$.
点评 本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
1.代数式2abc,-3x2+x,-$\frac{3}{x}$,2$\frac{1}{3}$中,单项式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.按某种标准把多项式分类,4x2-4与a3b+2ab2属于同一类,则下列多项式中也属于这一类的是( )
| A. | -x5+y3 | B. | 3x3+x+1 | C. | 2ab+cd+2 | D. | a4+3a3+2ab2+b3 |
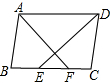 如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G
如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G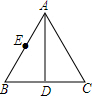 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.