题目内容
 点E是矩形ABCD的DC边上任意一点,AE的延长线交BC的延长线于点F,直线BE交△CEF外接圆⊙O于点G,连接CG、FG.
点E是矩形ABCD的DC边上任意一点,AE的延长线交BC的延长线于点F,直线BE交△CEF外接圆⊙O于点G,连接CG、FG.(1)求证:△ABE∽△GFC;
(2)若DE:CE=2:3,BH切⊙O于点H,且BH=2
| 10 |
(3)在(2)的条件下,若AB=BE,求⊙O面积.
考点:圆的综合题
专题:综合题
分析:(1)由对顶角相等得∠AEB=∠GEF,再由圆周角定理得∠GEF=∠GCF,则∠AEB=∠GCF,利用AB∥CD得∠BAE=∠CEF,由圆周角定理得∠CEF=∠CGF,则∠BAE=∠CGF,于是可根据相似三角形的判定方法得到△ABE∽△GFC;
(2)根据矩形的性质得AD∥BC,AD=BC,则可得到△ADE∽△FCE,利用相似比得
=
,所以
=
,设BC=2a,则CF=3a,BF=5a,再利用切割线定理得到(2
)2=2a•5a,解得a=2,所以CF=6,BC=4;
(3)设DE=2t,则CE=3t,DC=5t,利用矩形的性质得AB=CD=5t,则BA=BE=5t,在Rt△BCE中利用勾股定理计算出BC=4t,则4t=4,解得t=1,所以EC=3,
再在Rt△CEF中利用勾股定理计算出EF=3
,由于∠ECF=90°,根据圆周角定理得到EF为⊙O的直径,于是得到⊙O的半径=
,然后根据圆的面积公式求解.
(2)根据矩形的性质得AD∥BC,AD=BC,则可得到△ADE∽△FCE,利用相似比得
| AD |
| CF |
| 2 |
| 3 |
| BC |
| CF |
| 2 |
| 3 |
| 10 |
(3)设DE=2t,则CE=3t,DC=5t,利用矩形的性质得AB=CD=5t,则BA=BE=5t,在Rt△BCE中利用勾股定理计算出BC=4t,则4t=4,解得t=1,所以EC=3,
再在Rt△CEF中利用勾股定理计算出EF=3
| 5 |
3
| ||
| 2 |
解答:(1)证明:∵∠AEB=∠GEF,
而∠GEF=∠GCF,
∴∠AEB=∠GCF,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BAE=∠CEF,
而∠CEF=∠CGF,
∴∠BAE=∠CGF,
∴△ABE∽△GFC;
(2)解:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC
∴△ADE∽△FCE,
∴
=
=
,
∴
=
,
设BC=2a,则CF=3a,BF=5a,
∵BH切⊙O于点H,
∴BH2=BC•BF,即(2
)2=2a•5a,解得a=2,
∴CF=6,BC=4;
(3)解:设DE=2t,则CE=3t,DC=5t,
∵四边形ABCD为矩形,
∴AB=CD=5t,
∵BA=BE,
∴BE=5t,
在Rt△BCE中,BE=5t,CE=3t,
∴BC=
=4t,
∴4t=4,解得t=1,
∴EC=3,
在Rt△CEF中,CF=6,CE=3,
∴EF=
=3
,
∵∠ECF=90°,
∴EF为⊙O的直径,
∴⊙O的半径=
,
∴⊙O面积=π•(
)2=
.
而∠GEF=∠GCF,
∴∠AEB=∠GCF,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BAE=∠CEF,
而∠CEF=∠CGF,
∴∠BAE=∠CGF,
∴△ABE∽△GFC;
(2)解:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC

∴△ADE∽△FCE,
∴
| AD |
| CF |
| DE |
| EC |
| 2 |
| 3 |
∴
| BC |
| CF |
| 2 |
| 3 |
设BC=2a,则CF=3a,BF=5a,
∵BH切⊙O于点H,
∴BH2=BC•BF,即(2
| 10 |
∴CF=6,BC=4;
(3)解:设DE=2t,则CE=3t,DC=5t,
∵四边形ABCD为矩形,
∴AB=CD=5t,
∵BA=BE,
∴BE=5t,
在Rt△BCE中,BE=5t,CE=3t,
∴BC=
| BE2-CE2 |
∴4t=4,解得t=1,
∴EC=3,
在Rt△CEF中,CF=6,CE=3,
∴EF=
| CF2+CE2 |
| 5 |
∵∠ECF=90°,
∴EF为⊙O的直径,
∴⊙O的半径=
3
| ||
| 2 |
∴⊙O面积=π•(
3
| ||
| 2 |
| 45π |
| 4 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理、切割线定理三角形相似的判定与性质和矩形的性质;会勾股定理和相似比进行几何计算.

练习册系列答案
相关题目
 以各小正方形的顶点为顶点的三角形称为格点三角形,如图中的△ABC,请在图中画出与△ABC相似但不全等的三角形.
以各小正方形的顶点为顶点的三角形称为格点三角形,如图中的△ABC,请在图中画出与△ABC相似但不全等的三角形.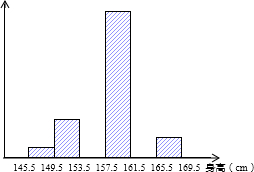 为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图).
为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图).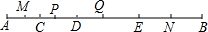 如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)
如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)