题目内容
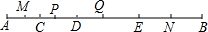 如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)
如图,点C,D,E将线段AB分成四个部分,且AC:CD:DE:EB=2:3:4:5,点M,P,Q,N分别是AC,CD,DE,EB的中点,且MN=21,求PQ的长度.(不要求写出每步的依据)考点:两点间的距离
专题:
分析:根据线段的比例,可设出未知数,根据线段中点的性质,可得MC=
AC=a,EN=
EB=
,PD=
CD=
,DQ=
DE=2a,根据线段的和差,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 5a |
| 2 |
| 1 |
| 2 |
| 3a |
| 2 |
| 1 |
| 2 |
解答:解:设AC=2a,CD=3a,DE=4a,EB=5a,
M,P,Q,N分别是AC,CD,DE,EB的中点,
MC=
AC=a,EN=
EB=
,PD=
CD=
,DQ=
DE=2a,
MC+CD+DE+EN=MN=21,
a+3a+4a+
a=21
a=2,
PD=3,DQ=4
PQ=PD+DQ=3+4=7.
M,P,Q,N分别是AC,CD,DE,EB的中点,
MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5a |
| 2 |
| 1 |
| 2 |
| 3a |
| 2 |
| 1 |
| 2 |
MC+CD+DE+EN=MN=21,
a+3a+4a+
| 5 |
| 2 |
a=2,
PD=3,DQ=4
PQ=PD+DQ=3+4=7.
点评:本题考查了两点间的距离,利用了线段的比例,线段中点的性质,线段的和差.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
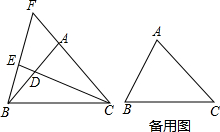 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F. 点E是矩形ABCD的DC边上任意一点,AE的延长线交BC的延长线于点F,直线BE交△CEF外接圆⊙O于点G,连接CG、FG.
点E是矩形ABCD的DC边上任意一点,AE的延长线交BC的延长线于点F,直线BE交△CEF外接圆⊙O于点G,连接CG、FG.