题目内容
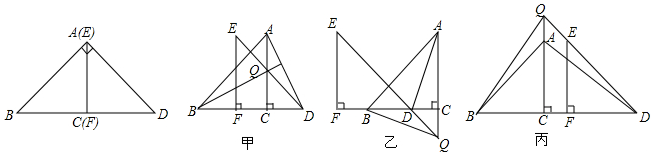
18.数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.请你阅读下面交流信息,解决所提出的问题.
展示交流:
小敏:满足条件的图形如图甲所示图形,延长BQ与AD交于点H.我们可以证明△BCQ≌△ACD,从而易得BQ=AD,BQ⊥AD.
小慧:根据图甲,当点F在线段BC上时,我们可以验证小敏的说法是正确的.但当点F在线段CB的延长线上(如图乙)或线段CB的反向延长线上(如图丙)时,我对小敏说法的正确性表示怀疑.
(1)请你帮助小慧进行分析,小敏的结论在图乙、图丙中是否成立?请说明理由.
(选择图乙或图丙的一种情况说明即可).
(2)小慧思考问题的方式中,蕴含的数学思想是分类讨论思想.
分析 (1)利用等腰直角三角形的性质结合全等三角形的判定与性质得出BQ=AD,BQ⊥AD;
(2)利用已知条件分类得出,体现数学中的分类讨论思想.
解答 解:(1)成立,
理由:如图乙:由题意可得:∠FDE=∠QDC=∠ABC=∠BAC=45°,
则DC=QC,AC=BC,
在△ADC和△BQC中
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCQ}\\{DC=CQ}\end{array}\right.$,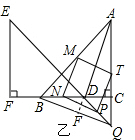
∴△ADC≌△BQC(SAS),
∴AD=BQ,∠DAC=∠QBC,
延长AD交BQ于点F,
则∠ADC=∠BDF,
∴∠BFD=∠ACD=90°,
∴AD⊥BQ;
(2)小慧思考问题的方式中,蕴含的数学思想是:分类讨论思想;
故答案是:分类讨论思想.
点评 此题主要考查了几何变换综合题,以及全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
7.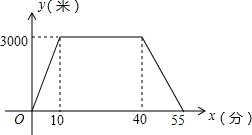 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )| A. | 娟娟同学与超市相距3000m | |
| B. | 娟娟同学去超市途中的速度是300m/min | |
| C. | 娟娟同学在超市逗留了30min | |
| D. | 娟娟同学从超市返回家比从家里去超市的速度快 |
 已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).
已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).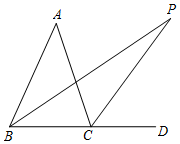 如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
 如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.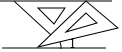 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )