题目内容
9.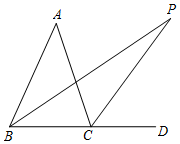 如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
分析 根据角平分线的定义可得∠CBP=$\frac{1}{2}$∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCP,然后整理即可得到∠P=$\frac{1}{2}$∠A,代入数据计算即可得解.
解答 解:∵BP平分∠ABC,
∴∠CBP=$\frac{1}{2}$∠ABC,
∵CP平分△ABC的外角,
∴∠DCP=$\frac{1}{2}$∠ACD=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCP中,由三角形的外角性质,∠DCP=∠CBP+∠P=$\frac{1}{2}$∠ABC+∠P,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠P,
∴∠P=$\frac{1}{2}$∠A=$\frac{1}{2}$×40°=20°.
点评 本题考查了三角形的外角性质的应用,能正确运用性质进行推理和计算是解此题的关键,注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
14.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
(2)如果a+b-c=m,观察上表猜想:$\frac{S}{l}$=$\frac{m}{4}$ (用含有m的代数式表示).
(3)证明(2)中的结论.
(1)填表:
| 三边a、b、c | a+b-c | $\frac{S}{l}$ |
| 3、4、5 | 2 | $\frac{1}{2}$ |
| 5、12、13 | 4 | 1 |
| 8、15、17 | 6 | $\frac{3}{2}$ |
(3)证明(2)中的结论.
 如图,点E、F分别在正方形ABCD的边BC、CD上,且BE=CF.
如图,点E、F分别在正方形ABCD的边BC、CD上,且BE=CF.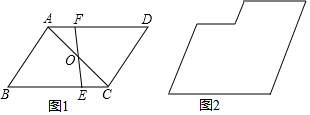
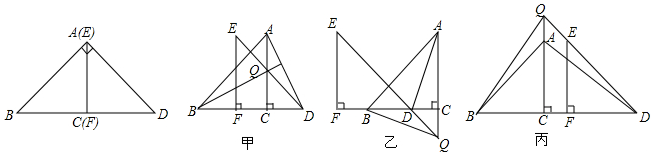
 如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)
如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是①.(填番号)