题目内容
16.化简求值:$(-\frac{1}{2}a+b)(-\frac{1}{2}a-b)(\frac{1}{4}{a^2}+{b^2})-{({a^2}+{b^2})^2}$,其中a=2,$b=-\frac{1}{2}$.分析 原式利用平方差公式及完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=($\frac{1}{4}$a2-b2)($\frac{1}{4}$a2+b2)-(a4+2a2b2+b4)=$\frac{1}{16}$a4-b4-a4-2a2b2-b4=-$\frac{15}{16}$a4-2b4-2a2b2,
当a=2,b=-$\frac{1}{2}$时,原式=-15-$\frac{1}{8}$-2=-17$\frac{1}{8}$.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.设a为实数(常数),已知直线l:y=ax-a-2,过点P(-1,0)作直线l的垂线,垂足为M,点O(0,0)为坐标原点,则线段OM长度的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{2}$-1 | C. | $\frac{2\sqrt{5}}{5}$ | D. | 1 |
11.能使等式$\sqrt{\frac{x}{x-2}}$=$\frac{\sqrt{x}}{\sqrt{x-2}}$成立的x取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x≥2 | D. | x≥0 |
6.若(x+m)与(x+3)的乘积不含x的项( )
| A. | 3 | B. | -3 | C. | 0 | D. | 1 |
 如图所示,△ABC的高BD、CE相交于点O,若∠A=60°,则∠BOC=120°.
如图所示,△ABC的高BD、CE相交于点O,若∠A=60°,则∠BOC=120°.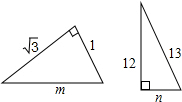 如图,m=2,n=5.
如图,m=2,n=5.