Question

4．设a为实数（常数），已知直线l：y=ax-a-2，过点P（-1，0）作直线l的垂线，垂足为M，点O（0，0）为坐标原点，则线段OM长度的最小值为（　　）

• A． $\frac{1}{3}$
• B． $\sqrt{2}$-1
• C． $\frac{2\sqrt{5}}{5}$
• D． 1

Answer 1

分析 由y=ax-a-2=（x-1）a-2可知直线l必过定点（1，-2），以定点和P点间的线段为圆心，以线段的长为直径，交y轴于M₁、M₂，则OM₁是OM的最小值，据此即可得答案．

解答 解：∵y=ax-a-2=（x-1）a-2，
∴当a的系数x-1=0，即x=1时，对于任意实数a，直线y=ax-a-2，都经过应该定点Q（1，-2），
如图，以P（-1，0）和Q（1，-2）之间的线段为直径画弧，交y轴于M₁、M₂，则OM₁最小，OM₂最大，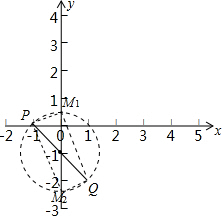

∵P（-1，0），Q（1，-2），
∴PQ=$\sqrt{（-1-1）^{2}+（0-2）^{2}}$=2$\sqrt{2}$，
∴圆心为（0，-1），半径为$\sqrt{2}$，
∴OM₁=$\sqrt{2}$-1，OM₂=$\sqrt{2}$+1，
∴OM长度的最小值为$\sqrt{2}$-1，
故选：B．

点评 本题考查了一次函数图象上点的坐标特征，把握住a的系数为0得知直线必过的定点，以定点和P点间的线段为圆心，以线段的长为直径，交y轴于M₁、M₂，得出OM₁是OM的最小值是解题的关键．