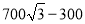题目内容
20. 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足(1)求证:△BCF≌△CAE;
(2)根据第(1)题的结论判断线段AE、BF、EF的大小关系.并说明理由.
分析 (1)利用∠BAC=∠ABC,得到AC=CB,利用HL证明Rt△CAE≌Rt△BCF.
(2)由Rt△CAE≌Rt△BCF,得到AE=CF,CE=BF,再根据CF=CE+EF,即可解答.
解答 解:(1)∵∠BAC=∠ABC,
∴AC=CB,
∵AE⊥CF,BF⊥CF,
∴∠AEC=∠CFB=90°,
在Rt△CAE和Rt△BCF中,
$\left\{\begin{array}{l}{AC=CB}\\{CE=BF}\end{array}\right.$,
∴Rt△CAE≌Rt△BCF.
(2)∵Rt△CAE≌Rt△BCF.
∴AE=CF,CE=BF,
∵CF=CE+EF,
∴AE=BF+EF.
点评 本题考查了全等三角形的性质与判定定理,解决本题的关键是证明Rt△CAE≌Rt△BCF.

练习册系列答案
相关题目
 如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.
如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.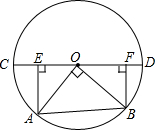 如图,CD为⊙O的直径,OA,OB是⊙O的半径,OA⊥OB,作AE⊥CD于E,BF⊥CD于F,已知AB=5$\sqrt{2}$.求CE+AE+BF+DF的值.
如图,CD为⊙O的直径,OA,OB是⊙O的半径,OA⊥OB,作AE⊥CD于E,BF⊥CD于F,已知AB=5$\sqrt{2}$.求CE+AE+BF+DF的值.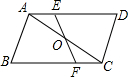 如图,已知AB=CD,AD=BC,点O为AC的中点,过点O的直线分别与AD,BC交于点E,F,求证:AE=CF.
如图,已知AB=CD,AD=BC,点O为AC的中点,过点O的直线分别与AD,BC交于点E,F,求证:AE=CF.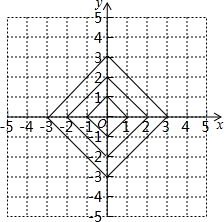 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.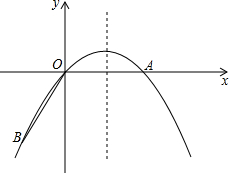 如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
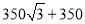 B.
B. 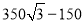 C. 1000 D.
C. 1000 D.