题目内容
14. 如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.
如图,AB=AC,DC=DB,∠A+∠D=180°,求证:∠B=∠C=90°.
分析 根据多边形内角和定理求出∠C+∠B=180°,根据SSS证△ACD≌△ABD,推出∠B=∠C即可.
解答 证明:∵∠A+∠D=180°,
∴∠C+∠B=360°-180°=180°,
连接AD,
∵在△ACD和△ABD中
$\left\{\begin{array}{l}{AC=AB}\\{AD=AD}\\{DC=DB}\end{array}\right.$
∴△ACD≌△ABD(SSS),
∴∠B=∠C,
∵∠C+∠B=180°,
∴∠B=∠C=90°.
点评 本题考查了多边形内角和定理,全等三角形的性质和判定的应用,能求出∠B=∠C是解此题的关键.

练习册系列答案
相关题目
9.下列函数(1)y=x;(2)y=2x-1;(3)y=$\frac{1}{x}$;(4)x+y=1中,是一次函数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
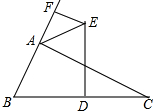 如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13. 如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.
如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.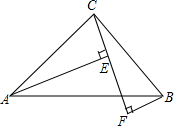 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足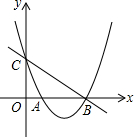 已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.
已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.