题目内容
5.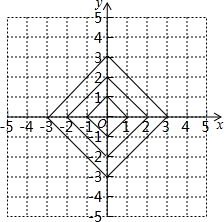 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,如图,由里向外数的第2各正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1,2,3,…得到的,请你观察图形,猜想由里向外第12个正方形四条边上的整点个数为48.
分析 根据第一个正方形可以得到整点个数为4,第二个正方形可知除顶点外每条边上的整点个数为1,故第二个正方形四条边上的整点个数为:4×1+4,同理可知,第三个正方形四条边上的整点个数为:4×2+4,从而可以得到第12个正方形四条边上的整点个数为.
解答 解:根据题意可得,第一个正方形四条边上的整点个数为:4;
第二个正方形四条边上的整点个数为:4×1+4=8;
第三个正方形四条边上的整点个数为:4×2+4=12;
由此可得,由里向外第12个正方形四条边上的整点个数为:4×11+4=48.
故答案为:48.
点评 本题考查规律性:点的坐标,解题的关键是观察各个正方形,能发现正方形四条边上的整点数的规律.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
20.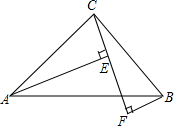 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
(1)求证:△BCF≌△CAE;
(2)根据第(1)题的结论判断线段AE、BF、EF的大小关系.并说明理由.
 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足(1)求证:△BCF≌△CAE;
(2)根据第(1)题的结论判断线段AE、BF、EF的大小关系.并说明理由.
10.若a是有理数,则下列判断正确的是( )
| A. | |a|是正数 | B. | -a是负数 | C. | |a|是正数或0 | D. | |-a|是负数或0 |
 如图:两个同心圆,其中大圆的弦AD交小圆于C、D两点那么:AB与CD相等吗?为什么?
如图:两个同心圆,其中大圆的弦AD交小圆于C、D两点那么:AB与CD相等吗?为什么?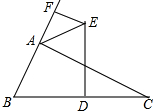 如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13.
如图,已知△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=3,AB=7,那么AC长是13. 如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD.
如图,直线l交线段AB于点P,AC⊥l,BD⊥l,垂足分别为C、D,M是AB的中点,求证:MC=MD. 如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD.
如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD. <n+1,则n的值为( )
<n+1,则n的值为( )