题目内容
15.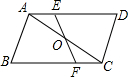 如图,已知AB=CD,AD=BC,点O为AC的中点,过点O的直线分别与AD,BC交于点E,F,求证:AE=CF.
如图,已知AB=CD,AD=BC,点O为AC的中点,过点O的直线分别与AD,BC交于点E,F,求证:AE=CF.
分析 根据已知条件判断四边形ABCD是平行四边形,根据平行四边形的对边平行可得AD∥BC,再根据两直线平行,内错角相等可得∠EAO=∠FCO,然后利用“角边角”证明△AOE和△COF全等,最后根据全等三角形对应边相等证明即可.
解答 证明:∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴AE=CF.
点评 本题考查了全等三角形的判定与性质,平行四边形的判定与性质,平行线的性质,难点在于判断出四边形ABCD是平行四边形然后求出三角形全等的条件.

练习册系列答案
相关题目
9.下列函数(1)y=x;(2)y=2x-1;(3)y=$\frac{1}{x}$;(4)x+y=1中,是一次函数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.
如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF. 如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC.
如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC.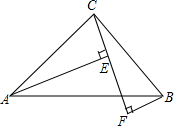 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数:y=-$\frac{1}{20}$x+8.