题目内容
9.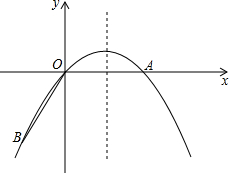 如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.
如图,点A在x轴上,OA=6,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;
(2)求经过A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形的面积是9?若存在,求出过点P的坐标;若不存在,请说明理由.
分析 (1)根据旋转的性质,可得OB=OA=6,∠BOC=120°,根据直角三角形的性质,可得BC,OC的长;
(2)根据抛物线与x轴的交点坐标,可得抛物线的解析式,根据待定系数法,可得答案;
(3)根据三角形的面积,可得P到BC的距离为3,根据平行线间的距离相等,可得平行OB且到OB的距离等于3的两条直线,根据自变量与函数值的对应关系,可得P点坐标.
解答 解:(1)如图1:
由OA=6,将线段OA绕点O顺时针旋转120°至OB的位置,得
OB=OA=6,∠BOC=120°.
∠BOC=120°-90°=30°
∴BC=$\frac{1}{2}$OB=3,
OC=3$\sqrt{3}$,
∴B(-3,-3$\sqrt{3}$)
(2)因为抛物线与x轴交于O、A(6,0),
设抛物线的解析式为y=ax(x-6),把点B(-3,-3$\sqrt{3}$)代入得-3a(-3-6)=-3$\sqrt{3}$,
解得:a=-$\frac{{\sqrt{3}}}{9}$.
所以抛物线的解析式为y=-$\frac{{\sqrt{3}}}{9}$x(x-6)=-$\frac{{\sqrt{3}}}{9}$x2+$\frac{{2\sqrt{3}}}{3}$x.
(3)答:符合条件的点P存在
设直线OB的解析式为:y=kx,
把点了B(-3,-3$\sqrt{3}$)代入解得:k=$\sqrt{3}$
∴直线OB的解析式为:y=$\sqrt{3}$x,
∵S△BOP=9,
∴点P到OB的距离是:(9×2)÷6=3
如图2:
设点E到OB的距离EF=3,
∵∠BOE=30°,
∴OE=2EF=6
∴到直线OB的距离为3的直线解析式分别是:y=$\sqrt{3}$x-6 或y=$\sqrt{3}$x+6
抛物线的对称轴是直线x=$\frac{1}{2}$×6=3,
∴把x=3分别代入y=$\sqrt{3}$x-6、y=$\sqrt{3}$x+6得y 1=3$\sqrt{3}$-6,y 2=3$\sqrt{3}$+6,
即符合条件的点P的坐标是:P1(3,3$\sqrt{3}$-6),P2(3,3$\sqrt{3}$+6).
点评 本题考查了二次函数综合题,(1)利用了旋转的性质,直角三角形的性质;(2)利用待定系数法求函数解析式,关键是设出与X轴交点的解析式;(3)利用平行线间的距离相等得出平行OB且到OB的距离等于3的两条直线是解题关键.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案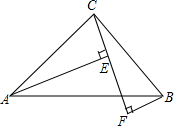 如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足
如图,已知:∠BAC=∠ABC,CE=BF,AE⊥CF,BF⊥CF,C、E、F分别为垂足(1)求证:△BCF≌△CAE;
(2)根据第(1)题的结论判断线段AE、BF、EF的大小关系.并说明理由.
在最近的五次数学过关测试中,小聪和小明的成绩如下表:(单位:分)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
小聪 | 75 | 80 | 100 | 90 | 80 |
小明 | 70 | 85 | 95 | 95 | 80 |
(1)完成下表:
平均成绩(分) | 中位数(分) | 众数(分) | |
小聪 | 85 | ______ | ______ |
小明 | ______ | 85 | 95 |
(2)在这五次测试中,哪位同学的成绩比较稳定?请说明理由.
 如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD.
如图,⊙O1与⊙O2交于A、B两点,P是⊙O1上的点,连接PA、PB交⊙O2于C、D,求证:PO1⊥CD.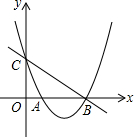 已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.
已知抛物线C1:y=x2-4x+3与x轴交于A,B两点,与y轴交于C点,平移直线BC,至PQ,点P在对称轴上,点Q在第一象限的抛物线上,且CP=QB,求Q点的坐标.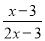 的值为0,则x的值为______.
的值为0,则x的值为______.