题目内容
已知：二次函数y=-x2-2x+m的部分图象如图所示，则关于x的一元二次方程-x2-2x+m=0的解为（ ）| A、1 | B、3 | C、2 | D、0 |
考点：抛物线与x轴的交点
专题：
分析：根据二次函数的图象得出抛物线与x轴的交点，进而可得出结论．
解答：解：∵由图可知，抛物线的对称轴为x=-1，抛物线与x轴的一个交点为-3，
∴另一个交点=2×（-1）+3=1，
∴关于x的一元二次方程-x2-2x+m=0的解为x1=-3，x2=1．
故选A．
∴另一个交点=2×（-1）+3=1，
∴关于x的一元二次方程-x2-2x+m=0的解为x1=-3，x2=1．
故选A．
点评：本题考查的是抛物线与x轴的交点问题，熟知二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键．
练习册系列答案
相关题目
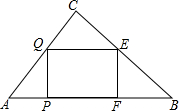如图，在Rt△ABC中，∠C=90°，AC=30cm，BC=40m，矩形EFPQ的四个定点分别在三边上．设EF=xm，矩形EFPQD的面积为ym2，当x为何值时，y的值最大？最大值是多少？
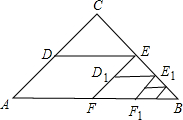如图，△ABC中，∠C=90°，AC=BC=2，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的面积记作S2．照此规律作下去，则S2012=
如图，一只蚂蚁从长、宽都是3，高是8的长方体纸箱的点A沿纸箱外表面爬到点B，那么它所行的最短路线的长是多少？下列命题中，是真命题的是（ ）
| A、一个角的补角大于这个角 |
| B、面积相等的两个三角形全等 |
| C、三角形的三条高线相交于三角形内一点 |
| D、成轴对称的两个图形是全等图形 |
若α为锐角，且cosα=
，则tanα为（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
运用等式性质进行的变形，正确的是（ ）
| A、如果a=b，那么a+2=b+3 | ||||
| B、如果a=b，那么a-2=b-3 | ||||
C、如果
| ||||
| D、如果a2=3a，那么a=3 |