题目内容
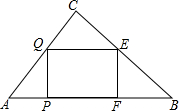 如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=40m,矩形EFPQ的四个定点分别在三边上.设EF=xm,矩形EFPQD的面积为ym2,当x为何值时,y的值最大?最大值是多少?
如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=40m,矩形EFPQ的四个定点分别在三边上.设EF=xm,矩形EFPQD的面积为ym2,当x为何值时,y的值最大?最大值是多少?考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:作CH⊥AB于H,交DG于T,设QE=z,根据△CQG∽△CAB,即可利用对应边的比相等,利用x表示出z的值,则矩形的面积即可利用x表示,利用二次函数的性质求解.
解答: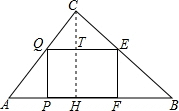 解:作CH⊥AB于H,交DG于T,设QE=z,
解:作CH⊥AB于H,交DG于T,设QE=z,
在直角△ABC中,AB=
=5.
∴AB•CH=AC•BC,
∴5CH=3×4,
∴CH=2.4.
∵四边形QEFP是矩形,
∴DG∥EF,TH=DE,
∴△CQG∽△CAB,
∴
=
,
∴
=
,
∴z=5-
x,
设矩形的面积为y=xz=x(5-
x)
即y=-
x2+5x,
则当x=
=
时,y最大=-
×
+5×
=3.
 解:作CH⊥AB于H,交DG于T,设QE=z,
解:作CH⊥AB于H,交DG于T,设QE=z,在直角△ABC中,AB=
| AC2+BC2 |
∴AB•CH=AC•BC,
∴5CH=3×4,
∴CH=2.4.
∵四边形QEFP是矩形,
∴DG∥EF,TH=DE,
∴△CQG∽△CAB,
∴
| CT |
| CH |
| QE |
| AB |
∴
| 2.4-x |
| 2.4 |
| z |
| 5 |
∴z=5-
| 25 |
| 12 |
设矩形的面积为y=xz=x(5-
| 25 |
| 12 |
即y=-
| 25 |
| 12 |
则当x=
| 5 | ||
|
| 6 |
| 5 |
| 25 |
| 12 |
| 36 |
| 25 |
| 6 |
| 5 |
点评:本题是二次函数与矩形的综合应用,求图形的面积的最大值问题,常用的方法就是转化为函数问题,利用函数的性质求解.

练习册系列答案
相关题目
抛物线y=3x2-4x+1与坐标轴的交点个数为( )
| A、0 | B、1 | C、2 | D、3 |
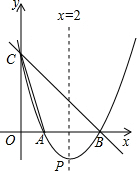 如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2. 如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系.
如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系. 如图,△ABC中,AB=10,AC=18,AD是角平分线,且AD=AB,则CD=
如图,△ABC中,AB=10,AC=18,AD是角平分线,且AD=AB,则CD= 已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( )
已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( )