题目内容
若α为锐角,且cosα=
,则tanα为( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:同角三角函数的关系
专题:
分析:根据cosα=
,设出关于两边的代数表达式,再根据勾股定理求出第三边长的表达式即可推出tanα的值.
| 4 |
| 5 |
解答: 解:设∠A=α,
解:设∠A=α,
∵cosα=
,
∴设AC=4,则AB=5,
根据勾股定理,得:AC=
=
=3,
∴tanα=
=
.
故选C.
 解:设∠A=α,
解:设∠A=α,∵cosα=
| 4 |
| 5 |
∴设AC=4,则AB=5,
根据勾股定理,得:AC=
| AB2-AC2 |
| 52-42 |
∴tanα=
| BC |
| AC |
| 3 |
| 4 |
故选C.
点评:本题考查了求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
已知(a2+b2)2-(a2+b2)-12=0,则a2+b2的值为( )
| A、-3 | B、4 |
| C、-3或4 | D、3或-4 |
3点半钟时,钟表的时针与分针的夹角是( )
| A、30° | B、45° |
| C、60° | D、75° |
-(x-2y+3z)去括号后的结果为( )
| A、x-2y+3z |
| B、-x+2y-3z |
| C、x+2y-3z |
| D、-x+2y+3z |
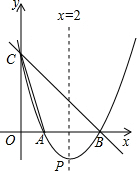 如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2. 已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( )
已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( ) 如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证:
如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证: