题目内容
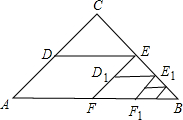 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2012=
如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2012=考点:相似多边形的性质
专题:规律型
分析:利用平行线分线段成比例定理得出S1=1,进而求出S2=
,同理可得:S3=
,即可得出答案.
| 1 |
| 4 |
| 1 |
| 42 |
解答:解:∵∠C=90°,AC=BC=2,
∴AB=2
,
∵取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,
∴AF=
AB,DE=
,
则四边形EDAF的面积为:S1=
×
=1,
∵取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,
∴
=
,
∴S2=
,
同理可得:S3=
,
则S2012=
.
故答案为:
.
∴AB=2
| 2 |
∵取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,
∴AF=
| 1 |
| 2 |
| 2 |
则四边形EDAF的面积为:S1=
| 2 |
| ||
| 2 |
∵取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,
∴
| DE |
| D1E1 |
| 1 |
| 2 |
∴S2=
| 1 |
| 4 |
同理可得:S3=
| 1 |
| 42 |
则S2012=
| 1 |
| 42011 |
故答案为:
| 1 |
| 42011 |
点评:此题主要考查了相似多边形的性质,得出S的变化规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y=3x2-4x+1与坐标轴的交点个数为( )
| A、0 | B、1 | C、2 | D、3 |
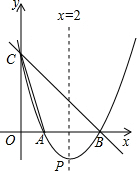 如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2. 如图,△ABC中,AB=10,AC=18,AD是角平分线,且AD=AB,则CD=
如图,△ABC中,AB=10,AC=18,AD是角平分线,且AD=AB,则CD= (1)解方程:2x2-3x=0;
(1)解方程:2x2-3x=0; 已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( )
已知:二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程-x2-2x+m=0的解为( ) 如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证:
如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证: