题目内容
如图,点P(-3,2)处的一只蚂蚁沿水平方向向右爬行了5个单位长度后的坐标为
.
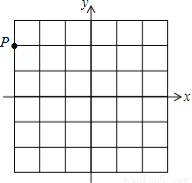
 (2,2)。
【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加。上下平移只改变点的纵坐标,下减上加。因此,蚂蚁沿水平方向向右爬行5个单位长度后,横坐标为:-3+5=2,纵坐标不变,所以爬行后的坐标为(2,2)。
(2,2)。
【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加。上下平移只改变点的纵坐标,下减上加。因此,蚂蚁沿水平方向向右爬行5个单位长度后,横坐标为:-3+5=2,纵坐标不变,所以爬行后的坐标为(2,2)。
练习册系列答案
相关题目
如图,已知线段AB。

(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
 【解析】
(1)作图如下:
(2)证明:根据题意作出图形如图,
∵点M、N在线段AB的垂直平分线l上,
∴AM=BM,AN=BN。
又 ∵MN=MN,∴△AMN≌△BMN(SSS)。
∴∠MAN=∠MBN。
【解析】(1)根据线段垂直平分线的性质作图。
(2)根据线段垂直平分线上的点到线段两端距离相等的性质,可得AM=BM,AN=BN。MN是公共边,从而...
【解析】
(1)作图如下:
(2)证明:根据题意作出图形如图,
∵点M、N在线段AB的垂直平分线l上,
∴AM=BM,AN=BN。
又 ∵MN=MN,∴△AMN≌△BMN(SSS)。
∴∠MAN=∠MBN。
【解析】(1)根据线段垂直平分线的性质作图。
(2)根据线段垂直平分线上的点到线段两端距离相等的性质,可得AM=BM,AN=BN。MN是公共边,从而... 分解因式:
(1)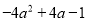 (2)
(2) 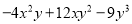
(3)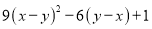 (4)
(4) 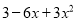
(5)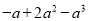 (6)
(6) 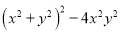
(7)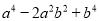 8)
8)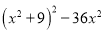
(9)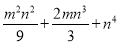 (10)
(10)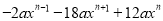
 (1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
...
(1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
... 若非零实数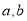 满足
满足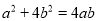 ,则
,则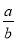 的值为( )
的值为( )
A. -2 B. 2 C. 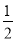 D.
D. 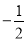
 B
【解析】试题解析:把a2+4b2=4ab,变形得:()2-4•+4=0,即(-2)2=0,
解得: =2,
故选B
B
【解析】试题解析:把a2+4b2=4ab,变形得:()2-4•+4=0,即(-2)2=0,
解得: =2,
故选B 已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
 (1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(...
(1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(... 将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
 D
【解析】点A(-2,-3)向右平移3个单位长度所得到的点B的坐标为(1,-3),故点B在第四象限.
D
【解析】点A(-2,-3)向右平移3个单位长度所得到的点B的坐标为(1,-3),故点B在第四象限. 将四边形ABCD平移后得到四边形A′B′C′D′,已知点A(-1,2)的对应点为A′(-7,10).若将四边形A′B′C′D′看成由四边形ABCD沿A到A′的方向一次平移得到的,则平移的距离为____.
 10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10.
10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10. 已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为_____.
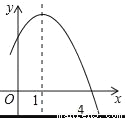
 x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线...
x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线... 等腰三角形的对称轴是______.
 顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线.
顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线. 
