��Ŀ����
��֪���κ���y=��x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η��̩�x2+2x+m=0�Ľ�Ϊ_____��
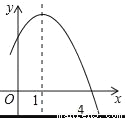
 x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������...
x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����ͼ���У������ĶԳ�ͼ�ε���( )
A.  B.
B.  C.
C.  D.
D. 
 A
���������������ĶԳƵĶ����ֻ֪��Aѡ����ϣ���ѡA.
A
���������������ĶԳƵĶ����ֻ֪��Aѡ����ϣ���ѡA. ��ͼ����P����3��2������һֻ������ˮƽ��������������5����λ���Ⱥ������Ϊ
�� ����
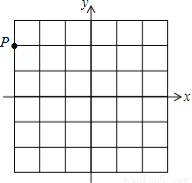
 ��2��2����
�����������������ƽ�Ʊ仯�Ĺ��ɣ�����ƽ��ֻ�ı��ĺ����꣬����Ҽӡ�����ƽ��ֻ�ı��������꣬�¼��ϼӡ���ˣ�������ˮƽ������������5����λ���Ⱥ�����Ϊ����3��5��2�������겻�䣬�������к������Ϊ��2��2����
��2��2����
�����������������ƽ�Ʊ仯�Ĺ��ɣ�����ƽ��ֻ�ı��ĺ����꣬����Ҽӡ�����ƽ��ֻ�ı��������꣬�¼��ϼӡ���ˣ�������ˮƽ������������5����λ���Ⱥ�����Ϊ����3��5��2�������겻�䣬�������к������Ϊ��2��2���� ������A(1��3)����ƽ��2����λ��������ƽ��4����λ�õ�B�����B������Ϊ( )
A. (��2����1) B. (��1��0) C. (��1����1) D. (��2��0)
 C
���������ߵ�A��1��3������ƽ��2����λ��������ƽ��4����λ�õ���B��
���B�ĺ�����Ϊ1?2��?1��������Ϊ3?4��?1��
��B��������?1��?1����
��ѡC��
C
���������ߵ�A��1��3������ƽ��2����λ��������ƽ��4����λ�õ���B��
���B�ĺ�����Ϊ1?2��?1��������Ϊ3?4��?1��
��B��������?1��?1����
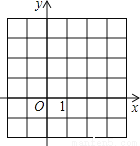
��ѡC�� ��1����������ϵ�л������κ���y=x2��2x�Ĵ���ͼ��
��2�����ݷ��̵ĸ��뺯��ͼ��Ĺ�ϵ��������x2��2x=1�ĸ���ͼ�Ͻ��Ƶı�ʾ��������㣩��
��3���۲�ͼ��ֱ��д������x2��2x=1�ĸ�������ȷ��0.1��
 ��������
��1������ͼ��
y=x2��2x=��x��1�� 2��1��
�������㣬������x��Ľ��㣬ͼ��⻬��
��2����ȷ������M��N��
��3��д�����̵ĸ�Ϊ��0.4��2.4��
��������
��1��ȷ�������������x��y�ύ�㣬����ͼ�Σ�
��2������x2��2x=1�ĸ����Ƕ��κ���y=x2��2x�ĺ���ֵΪ1ʱ�ĺ�����x��ֵ��
��3���۲�ͼ���֪ͼ��ĺ����꼴...
��������
��1������ͼ��
y=x2��2x=��x��1�� 2��1��
�������㣬������x��Ľ��㣬ͼ��⻬��
��2����ȷ������M��N��
��3��д�����̵ĸ�Ϊ��0.4��2.4��
��������
��1��ȷ�������������x��y�ύ�㣬����ͼ�Σ�
��2������x2��2x=1�ĸ����Ƕ��κ���y=x2��2x�ĺ���ֵΪ1ʱ�ĺ�����x��ֵ��
��3���۲�ͼ���֪ͼ��ĺ����꼴... ��֪����y=��x-a����x-b��������a��b����ͼ����ͼ��ʾ������y=ax+b��ͼ�������ȷ���ǣ�������
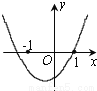
A. 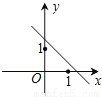 B.
B. 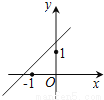 C.
C. 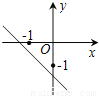 D.
D. 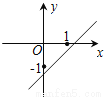
 D
������������ͼ��ɵó����̣�x-a����x-b��=0������ʵ����Ϊa��b����һ��һ���������ľ���ֵ��
��a��b����a��0��b��0��
�ຯ��y=ax+b��ͼ����һ�����������ޣ�
��ѡ��D��
D
������������ͼ��ɵó����̣�x-a����x-b��=0������ʵ����Ϊa��b����һ��һ���������ľ���ֵ��
��a��b����a��0��b��0��
�ຯ��y=ax+b��ͼ����һ�����������ޣ�
��ѡ��D�� ��ͼ����֪��������x���һ������A��1��0�����Գ�����x= -1�������������x�����һ���������ǣ�������

A. ��-3��0�� B. ��-2��0�� C. x= -3 D. x= -2
 A
����������������x�����һ����ΪB(b��0)��
����������x���һ������A(1��0)���Գ�����x����1���ࣽ��1��
���b����3����B(��3��0)��
A
����������������x�����һ����ΪB(b��0)��
����������x���һ������A(1��0)���Գ�����x����1���ࣽ��1��
���b����3����B(��3��0)�� ���и�ʽ����ȫƽ��ʽ���ǣ�������
A. x2+2x��1 B. 1+x2 C. x2+xy+1 D. x2��x+0.25
 D
��������A. x2+2x��1����ƽ����ķ��Ų�һ�£�������ȫƽ��ʽ��
B. 1+x2ȱ���������������ȫƽ��ʽ��
C. x2+xy+1ȱ���������������ȫƽ��ʽ��
D. x2��x+0.25=(x-0.5)2,����ȫƽ��ʽ��
��ѡD.
D
��������A. x2+2x��1����ƽ����ķ��Ų�һ�£�������ȫƽ��ʽ��
B. 1+x2ȱ���������������ȫƽ��ʽ��
C. x2+xy+1ȱ���������������ȫƽ��ʽ��
D. x2��x+0.25=(x-0.5)2,����ȫƽ��ʽ��
��ѡD. ��ͼ��ʾ��A��B����֮����һ��ɽ������ԭ����A�ص�B����Ҫ��C��������A��C��B��ʻ���ֿ�ͨ����������ֱ����ֱ��AB��ʻ����֪AC��10 km����A��30�㣬��B��45�㣬��������ͨ��������A�ص�B�ر�ԭ�����߶���ǧ��?(�����ȷ��0.1 km,�ο����ݣ� 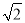 ��1.41��
��1.41�� 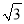 ��1.73)
��1.73)
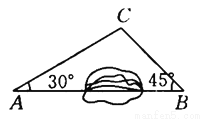
 ������ͨ��������A�ص�B�ر�ԭ������Լ3.4 km
���������������������C��AB�Ĵ���CD������ΪD����ֱ�ǡ�ACD��ֱ�ǡ�CBD�У���ֱ�����������CD��AD��BC���Ϳ��Եõ����ۣ�
�������������C��AB�Ĵ���CD������ΪD��
��AC=10km����A=30�㣬
��CD=AC=5��km����
AD==5��km����
��Rt��CDB��
�ߡ�B=45�㣬
...
������ͨ��������A�ص�B�ر�ԭ������Լ3.4 km
���������������������C��AB�Ĵ���CD������ΪD����ֱ�ǡ�ACD��ֱ�ǡ�CBD�У���ֱ�����������CD��AD��BC���Ϳ��Եõ����ۣ�
�������������C��AB�Ĵ���CD������ΪD��
��AC=10km����A=30�㣬
��CD=AC=5��km����
AD==5��km����
��Rt��CDB��
�ߡ�B=45�㣬
... 
