题目内容
等腰三角形的对称轴是______．
顶角平分线所在直线
【解析】一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴,如图所示：等腰三角形的对称轴是顶角平分线所在直线.
故答案是：顶角平分线所在直线.
练习册系列答案
相关题目
如图，点P（－3，2）处的一只蚂蚁沿水平方向向右爬行了5个单位长度后的坐标为
．
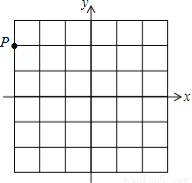
（2，2）。
【解析】根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，蚂蚁沿水平方向向右爬行5个单位长度后，横坐标为：－3＋5＝2，纵坐标不变，所以爬行后的坐标为（2，2）。 如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（ ）
A. （-3，0） B. （-2，0） C. x= -3 D. x= -2
A
【解析】抛物线与x轴的另一交点为B(b，0)，
∵抛物线与x轴的一个交点A(1，0)，对称轴是x＝－1，∴＝－1，
解得b＝－3，∴B(－3，0)． 下列各式是完全平方式的是（ ）
A. x2+2x﹣1 B. 1+x2 C. x2+xy+1 D. x2﹣x+0.25
D
【解析】A. x2+2x﹣1两个平方项的符号不一致，不是完全平方式；
B. 1+x2缺少两倍的项，不是完全平方式；
C. x2+xy+1缺少两倍的项，不是完全平方式；
D. x2﹣x+0.25=(x-0.5)2,是完全平方式；
故选D. 如图1，在一条河同一岸边有A和B两个村庄，要在河边修建码头M，使M到A和B的距离之和最短，试确定M的位置；
见解析
【解析】试题分析：利用轴对称，作点A关于直线l的对称点A′，连接A′B交直线l于点M，则点M即为所求点.
试题解析：所求点如下图所示：
∵两点之间线段最短，
∴需要能将AM、BM两边转化到一条直线上，
∴用轴对称可以办到，
求点M的位置的具体步骤如下：
①作作点A关于直线BC的轴对称点A’，
②连结A’B交BC于点M，
③连结AM，
... 如图，Rt△ABC中，∠C =90°，∠ABC的平分线BD交AC于D，若AD =5cm，CD =3cm，则点D到AB的距离DE是（ ）
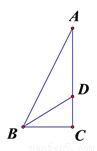
A. 5cm B. 4cm C. 3cm D. 2cm
C
【解析】∵点D到AB的距离是DE ，
∴DE⊥AB，
∵BD平分∠ABC，∠C =90°，
∴把Rt△BDC沿BD翻折后，点C在线段AB上的点E处，
∴DE=CD，
∵CD =3cm，
∴DE=3cm.
故选：C. 下列图形中，不一定是轴对称图形的是（ ）
A. 三角形 B. 射线 C. 角 D. 相交的两条直线
A
【解析】题中给出的四个选项中，射线以其所在直线为对称轴，角以其角平分线所在直线为对称轴，相交的两条直线以其夹角的平分线所在直线为对称轴.
故选：A. 如图所示，A，B两地之间有一座山，汽车原来从A地到B地需要经C地沿折线A—C—B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC＝10 km，∠A＝30°，∠B＝45°，则隧道开通后，汽车从A地到B地比原来少走多少千米?(结果精确到0.1 km,参考数据：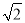 
≈1.41， 
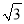≈1.73)
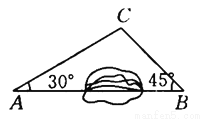
隧道开通后，汽车从A地到B地比原来少走约3.4 km
【解析】试题分析：过点C作AB的垂线CD，垂足为D，在直角△ACD和直角△CBD中，解直角三角形求出CD，AD，BC，就可以得到结论．
试题解析：过点C作AB的垂线CD，垂足为D．
∵AC=10km，∠A=30°，
∴CD=AC=5（km）．
AD==5（km）．
在Rt△CDB中，
∵∠B=45°，
... 在一幅长60cm，宽40cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是ycm2，设金色纸边的宽度为xcm2，那么y关于x的函数是（ ）
A. y=（60+2x）（40+2x） B. y=（60+x）（40+x）
C. y=（60+2x）（40+x） D. y=（60+x）（40+2x）
A
【解析】长是：60+2x，宽是：40+2x，
由矩形的面积公式得
则y=（60+2x）（40+2x）．
故选A．