题目内容
将四边形ABCD平移后得到四边形A′B′C′D′，已知点A(－1,2)的对应点为A′(－7,10)．若将四边形A′B′C′D′看成由四边形ABCD沿A到A′的方向一次平移得到的，则平移的距离为____.
10
【解析】因为平移后点A(－1,2)的对应点为A′(－7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10.
练习册系列答案
相关题目
如何作出一个图形的中心对称图形？
首先要先找到对称中心，对称点的连线一定经过对称中心，再就是两个图形是全等图形
【解析】【试题分析】本题目作一个图形的中心对称图形，方法见解析.
【试题解析】
首先要先找到对称中心，再将每个顶点与对称中心相连，并延长至等长，最后将得到每个对应点顺次连接即可. 下列各式中能用完全平方公式分解因式的是（ ）
A.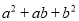 
B. 
C. 
D. 
C
【解析】A选项中间乘积项不是两底数积的2倍，故本选项错误； B选项不符合完成平方公式的特点，故本选项错误；C选项符合完全平方公式的特点；D选项不符合完成平方公式的特点，故本选项错误，
故选C． 如图，点P（－3，2）处的一只蚂蚁沿水平方向向右爬行了5个单位长度后的坐标为
．
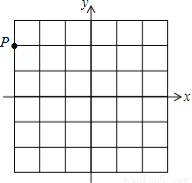
（2，2）。
【解析】根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，蚂蚁沿水平方向向右爬行5个单位长度后，横坐标为：－3＋5＝2，纵坐标不变，所以爬行后的坐标为（2，2）。 如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B(－3,3)也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．
(1)求点C的坐标和直线l1的解析式；
(2)若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；
(3)已知直线l2：y＝x＋b经过点B，与y轴交于点E，求△ABE的面积．
(1) C的坐标为(－2,1)，直线l1的解析式为y＝－2x－3；(2)点D在直线l1上；(3)△ABE的面积为13.5.
【解析】试题分析：（1）∵B（﹣3，3），将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，
∴﹣3+1=﹣2，3﹣2=1，∴C的坐标为（﹣2，1），设直线l1的解析式为y=kx+c，∵点B、C在直线l1上，∴代入得：，解得：k=﹣2，c=﹣3，∴直线... 若将点A(1，3)向左平移2个单位，再向下平移4个单位得到B，则点B的坐标为( )
A. (－2，－1) B. (－1，0) C. (－1，－1) D. (－2，0)
C
【解析】∵点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，
∴点B的横坐标为1?2＝?1，纵坐标为3?4＝?1，
∴B的坐标为（?1，?1）．
故选C． （1）请在坐标系中画出二次函数y=x2﹣2x的大致图象；
（2）根据方程的根与函数图象的关系，将方程x2﹣2x=1的根在图上近似的表示出来（描点）；
（3）观察图象，直接写出方程x2﹣2x=1的根．（精确到0.1）
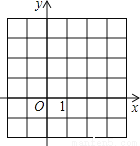
【解析】
（1）如下图，
y=x2﹣2x=（x﹣1） 2﹣1，
作出顶点，作出与x轴的交点，图象光滑．
（2）正确作出点M，N；
（3）写出方程的根为﹣0.4，2.4．
【解析】
（1）确定顶点坐标和与x轴y轴交点，作出图形；
（2）方程x2﹣2x=1的根就是二次函数y=x2﹣2x的函数值为1时的横坐标x的值；
（3）观察图象可知图象交点的横坐标即... 如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（ ）
A. （-3，0） B. （-2，0） C. x= -3 D. x= -2
A
【解析】抛物线与x轴的另一交点为B(b，0)，
∵抛物线与x轴的一个交点A(1，0)，对称轴是x＝－1，∴＝－1，
解得b＝－3，∴B(－3，0)． 下列图形中，不一定是轴对称图形的是（ ）
A. 三角形 B. 射线 C. 角 D. 相交的两条直线
A
【解析】题中给出的四个选项中，射线以其所在直线为对称轴，角以其角平分线所在直线为对称轴，相交的两条直线以其夹角的平分线所在直线为对称轴.
故选：A.